Question

【题目】已知函数f（x）=lnx﹣ ，g（x）=ax+b．
（1）若函数h（x）=f（x）﹣g（x）在（0，+∞）上单调递增，求实数a的取值范围；
（2）若直线g（x）=ax+b是函数f（x）=lnx﹣ 图象的切线，求a+b的最小值；
（3）当b=0时，若f（x）与g（x）的图象有两个交点A（x1 ， y1），B（x2 ， y2），求证：x1x2＞2e2 ． （取e为2.8，取ln2为0.7，取 为1.4）

Answer 1

【答案】
（1）解：h（x）=f（x）﹣g（x）= ，则 ，

∵h（x）=f（x）﹣g（x）在（0，+∞）上单调递增，∴对x＞0，都有 ，

即对x＞0，都有 ，

∵ ，∴a≤0，

故实数a的取值范围是（﹣∞，0]

（2）解：设切点 ，则切线方程为 ，

即 ，亦即 ，

令 ，由题意得 ，

令a+b=φ（t）=﹣lnt+t2﹣t﹣1，则 ，

当t∈（0，1）时，φ'（t）＜0，φ（t）在（0，1）上单调递减；

当t∈（1，+∞）时，φ'（t）＞0，φ（t）在（1，+∞）上单调递增，

∴a+b=φ（t）≥φ（1）=﹣1，故a+b的最小值为﹣1

（3）证明：由题意知 ， ，

两式相加得 ，

两式相减得 ，

即 ，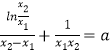

∴ ，

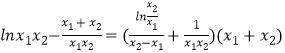即 ，

不妨令0＜x1＜x2，记 ，

令 ，则 ，

∴ 在（1，+∞）上单调递增，则 ，

∴ ，则 ，

∴ ，

又 ，

∴ ，即 ，

令 ，则x＞0时， ，

∴G（x）在（0，+∞）上单调递增，

又 ，

∴ ，

则 ，即

【解析】（1）把f（x）和g（x）代入h（x）=f（x）﹣g（x），求其导函数，结合h（x）在（0，+∞）上单调递增，可得对x＞0，都有h′（x）≥0，得到 ，由 得到a的取值范围；（2）设切点 ，写出切线方程，整理得到 ，令 换元，可得a+b=φ（t）=﹣lnt+t2﹣t﹣1，利用导数求其最小值；（3）由题意知 ， ，把a用含有x1 ， x2的代数式表示，得到 ，不妨令0＜x1＜x2 ， 记 ，构造函数 ，由导数确定其单调性，从而得到 ，即 ，然后利用基本不等式放缩得到 ，令 ，再由导数确定G（x）在（0，+∞）上单调递增，然后结合又 得到 ，即 ．