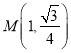题目内容
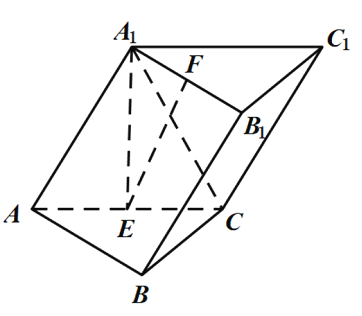
【题目】已知四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
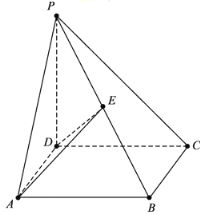
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)试判断![]() 所在直线与平面
所在直线与平面![]() 是否平行,并说明理由.
是否平行,并说明理由.
【答案】(1)证明见解析(2)![]() (3)AE与平面PCD不平行,详见解析
(3)AE与平面PCD不平行,详见解析
【解析】
(1)先根据条件证![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以可以证得平面
,所以可以证得平面![]() 平面
平面![]() .
.
(2)根据条件得![]() 两两垂直,以此建立空间直角坐标系,求出平面
两两垂直,以此建立空间直角坐标系,求出平面![]() 的法向量
的法向量![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,求出法向量
,求出法向量![]() ,根据公式求出两个法向量的余弦值,即可得出二面角
,根据公式求出两个法向量的余弦值,即可得出二面角![]() 的大小.
的大小.
(3)依题意可证![]() 平面
平面![]() ,则平面
,则平面![]() 的法向量为
的法向量为![]() ,又∵
,又∵![]() ,则
,则![]() 与
与![]() 不垂直,证得
不垂直,证得![]() 与平面
与平面![]() 不平行.
不平行.
(1)证明:∵![]() 是正方形
是正方形![]()
∵![]() ⊥平面
⊥平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]()
∵![]()
![]() 平面
平面![]()
∴![]() 平面
平面![]()
又∵![]()
![]() 平面
平面![]()
∴平面![]() 平面
平面![]()
(2)∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]()
又∵![]() 是正方形∴
是正方形∴![]()
∴![]() 两两垂直
两两垂直
∴以![]() 为原点如图建系,设
为原点如图建系,设![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]()
∴![]()
又∵![]() 平面
平面![]()
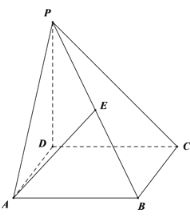
∴平面![]() 的法向量
的法向量![]()
设平面![]() 的法向量
的法向量![]()
则![]() ,
,![]()
∴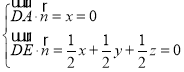
令![]() ,得
,得![]() ∴
∴![]()
∴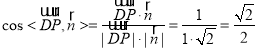
∴二面角![]() 的大小为
的大小为![]()
(3)∵![]() ,
,![]() ,
,![]()
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
∴平面![]() 的法向量为
的法向量为![]()
又∵![]()
∴![]() 与
与![]() 不垂直,∴
不垂直,∴![]() 与平面
与平面![]() 不平行
不平行

练习册系列答案
相关题目
【题目】某校高三实验班的60名学生期中考试的语文、数学成绩都在![]() 内,其中语文成绩分组区间是:
内,其中语文成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数
.其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
| |
语文人数 | 24 | 3 | |||
数学人数 | 12 | 4 |
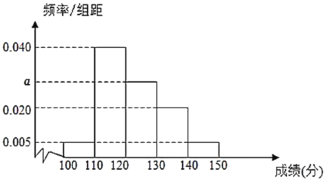
(1)求图中![]() 的值及数学成绩在
的值及数学成绩在![]() 的人数;
的人数;
(2)语文成绩在![]() 的3名学生均是女生,数学成绩在
的3名学生均是女生,数学成绩在![]() 的4名学生均是男生,现从这7名学生中随机选取4名学生,事件
的4名学生均是男生,现从这7名学生中随机选取4名学生,事件![]() 为:“其中男生人数不少于女生人数”,求事件
为:“其中男生人数不少于女生人数”,求事件![]() 发生的概率;
发生的概率;
(3)若从数学成绩在![]() 的学生中随机选取2名学生,且这2名学生中数学成绩在
的学生中随机选取2名学生,且这2名学生中数学成绩在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.