Question

【题目】设正项数列的前n项和为，已知

(1)求证：数列是等差数列，并求其通项公式

(2)设数列的前n项和为，且，若对任意都成立，求实数的取值范围．

Answer 1

【答案】（1）见证明；（2）

【解析】

（1）首先求出，利用与作差，化简即可得到为常数，进而可证明数列为等差数列，其首项为2，公差2，利用等差数列通项公式求出；

（2）结合（1）可得，利用裂项相消，即可求出数列的前项和为，代入，分离参数即可得到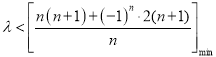，分别为奇数和偶数是的范围即可．

（1）证明:∵，且，

当时，，解得．

当时，有即，即．于是，

即．

∵，∴为常数

∴数列是为首项，为公差的等差数列，∴．

（2）由（1）可得： ，

∴

，即对任意都成立，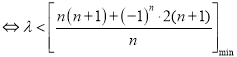

①当为偶数时，恒成立，

令，

，

在上为增函数，

②当为奇数时，恒成立，又，在为增函数，

∴由①②可知：

综上所述的取值范围为: