题目内容
10.已知[x]表示不大于x的最大整数,设函数f(x)=[log2x],得到下列结论:结论1:当1<x<2时,f(x)=0;
结论2:当2<x<4时,f(x)=1;
结论3:当4<x<8时,f(x)=2;
照此规律,得到结论10:当29<x<210时,f(x)=9.
分析 根据前3个结论,找到规律,即可得出结论.
解答 解:结论1:当1<x<2时,即20<x<21,f(x)=1-1=0;
结论2:当2<x<4时,即21<x<22,f(x)=2-1=1;
结论3:当4<x<8时,即22<x<23,f(x)=3-1=2,
通过规律,不难得到结论10:当29<x<210时,f(x)=10-1=9,
故答案为:当29<x<210时,f(x)=9.
点评 本题考查归纳推理,考查学生分析解决问题的能力,正确归纳是关键,属于基础题

练习册系列答案
相关题目
20.已知函数$f(x)=2sin({2x-\frac{π}{3}})-1$,在$[{0,\frac{π}{2}}]$随机取一个实数a,则f(a)>0的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
2.若根据10名儿童的年龄x(岁)与体重y(千克)数据用最小二乘法得到用年龄预测体重的回归方程$\hat y=2x+7$,已知这10名儿童的年龄分别是2,3,3,5,2,6,7,3,4,5,则这10名儿童的平均体重是( )
| A. | 15千克 | B. | 16千克 | C. | 17千克 | D. | 18千克 |
19.若MP和OM分别是角$\frac{7π}{6}$的正选线和余弦线,则( )
| A. | MP<OM<0 | B. | OM>0>MP | C. | OM<MP<0 | D. | MP>0>OM |
20.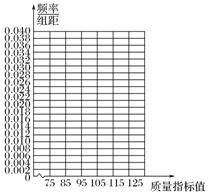 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
(1)作出这些数据的频数分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中间值来代表这种产品质量的指标值);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的85%”的规定?
 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中间值来代表这种产品质量的指标值);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的85%”的规定?
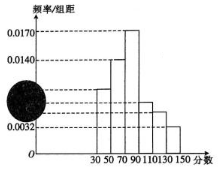 2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.
2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.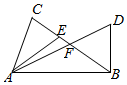 如图,F为线段BC的中点,CE=2EF,$DF=\frac{3}{5}AF$,设$\overrightarrow{AC}=a$,$\overrightarrow{AB}=b$,试用a,b表示$\overrightarrow{AE}$,$\overrightarrow{AD}$,$\overrightarrow{BD}$.
如图,F为线段BC的中点,CE=2EF,$DF=\frac{3}{5}AF$,设$\overrightarrow{AC}=a$,$\overrightarrow{AB}=b$,试用a,b表示$\overrightarrow{AE}$,$\overrightarrow{AD}$,$\overrightarrow{BD}$.