题目内容

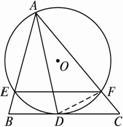
如图2-4-5，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂线，垂足为B，CB与⊙O相交于点E，AE平分∠CAB，且AE=2，求△ABC各边的长.

J

图2-4-5
答案：
解析：

 思路分析：∠BAE为弦切角，于是∠BAE=∠C，再由AE平分∠CAB和△ABC是直角三角形可得∠C的度数，进而解直角三角形即可.

解：∵AD为⊙O的切线，

∴∠BAE=∠C.

∵AE平分∠CAB，

∴∠BAC=2∠BAE.

又∵∠C+∠BAC=90°，

∴∠BAE=∠C=30°.

则有BE=1，AB=，BC=3，AC=.

深化升华 本题应用弦切角、解直角三角形的知识,为基础题型，求解此类题时，要注意弦切角在角的转换中的作用，本题正是由于这一条件，沟通了角之间的数量关系.


练习册系列答案
相关题目
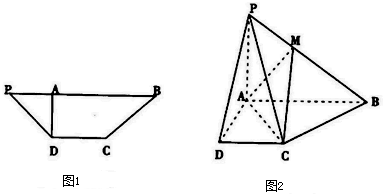在等腰梯形PDCB（图1）中，DC∥PB，PB=3DC=3，PD=
2
，DA⊥PB，垂足为A，将△PAD沿AD折起，使得PA⊥AB，得到四棱锥P-ABCD（图2）．在图2中完成下面问题：
（1）证明：平面PAD⊥平面PCD；
（2）点M在棱PB上，平面AMC把四棱锥P-ABCD分成两个几何体（如图2），当这两个几何体的体积之比VPM-ACDVM-ABC=5：4时，求
PM
MB
的值；
（3）在（2）的条件下，证明：PD‖平面AMC．
如图2-4-5,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F.求证:EF∥BC.?

图2-4-5

如图2-5-1,CE为⊙O的直径,PE为⊙O的切线,E为切点,PBA为⊙O的割线,交CE于D点,若CD=2,AD=3,BD=4,则PB等于(    )

图2-5-1

A.10                B.12                C.             D.20
如图2-4-5，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂线，垂足为B，CB与⊙O相交于点E，AE平分∠CAB，且AE=2，求△ABC各边的长.

J

图2-4-5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网