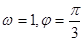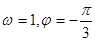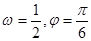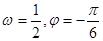题目内容
在同一平面直角坐标系中,函数y=cos(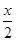 +
+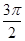 )(x∈[0,2π])的图象和直线y=
)(x∈[0,2π])的图象和直线y=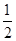 的交点个数是( )
的交点个数是( )
| A.0 | B.1 | C.2 | D.4 |
C.
解析试题分析:因为y=cos(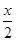 +
+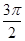 )(x∈[0,2π]),即
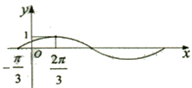
)(x∈[0,2π]),即 (x∈[0,2π])的图像是半个周期的图像,所以它与直线y=
(x∈[0,2π])的图像是半个周期的图像,所以它与直线y=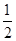 的交点有两个.
的交点有两个.
考点:三角函数的诱导公式及正弦函数的图像.
点评:本小题关键是利用诱导公式 把y=cos(
把y=cos(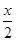 +
+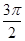 )(x∈[0,2π])转化为
)(x∈[0,2π])转化为 (x∈[0,2π])然后画出它的图像从图像上观察它与直线y=
(x∈[0,2π])然后画出它的图像从图像上观察它与直线y=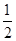 的交点个数.
的交点个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为得到函数 图像,只需将函数
图像,只需将函数 的图像( )
的图像( )
A.向右平移 个长度单位 个长度单位 | B.向左平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
若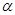 为第三象限角,则
为第三象限角,则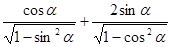 的值为 ( )
的值为 ( )
| A.-3 | B.-1 | C.1 | D.3 |
若函数 的取值分别是( )
的取值分别是( )
A. | B. |
C. | D. |
已知 是第三象限角,则
是第三象限角,则 是第( )象限角
是第( )象限角
| A.第一或第二象限角 | B.第二或第四象限角 |
| C.第一或第三象限角 | D.第三或第四象限角 |
已知 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,外接圆半径是
,外接圆半径是 ,,且满足条件
,,且满足条件 ,则
,则 的面积的最大值为 ( )
的面积的最大值为 ( )
A. | B. | C. | D. |
设 是△
是△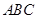 内一点,且
内一点,且 ,
, ,定义
,定义 ,其中
,其中 、
、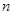 、
、 分别是△
分别是△ 、△
、△ 、△
、△ 的面积,若
的面积,若 , 则
, 则 的最小值是( )
的最小值是( )
| A.8 | B.9 | C. 16 | D.18 |
函数 定义域为
定义域为 ,值域为
,值域为 ,则
,则 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A. | B. | C. | D. |
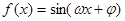 的图象(部分)如图所示,则
的图象(部分)如图所示,则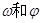 的取值是 ( )
的取值是 ( )