题目内容
(本小题满分13分)
公差不为零的等差数列 中,
中, ,且
,且 、
、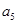 、
、 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列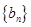 的前
的前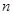 项的和
项的和 .
.
(1) (2)
(2)
解析试题分析:解:(1)设公差为 ,则
,则 解得
解得 ……4分
……4分
所以数列 的通项公式为
的通项公式为 ………6分
………6分
(2)由(1)可知, ,则
,则 ①
① ②
②
由①—②得: ………9分
………9分

 ………11分
………11分
所以, ………13分
………13分
考点:本试题考查了数列的通项公式和求和的知识点。
点评:熟练的运用等差数列和等比数列的概念来得到其通项公式,同时能利用错位相减法来表示得到数列的求和问题,这中求和的方法是高考中的常考的知识点,需要同学们熟练的运用,同时能根据通项公式的特点合理的选择求和的方法,也是需要总结和归纳的。属于中档题。

练习册系列答案
相关题目
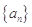 中,
中,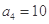 且
且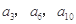 成等比数列,
成等比数列,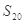 。
。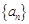 中,
中,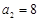 ,前10项的和
,前10项的和
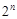 ,…项,按原来的顺序排成一个新的数列
,…项,按原来的顺序排成一个新的数列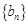 ,试求新数列
,试求新数列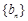 的前
的前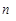 项和
项和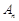 .
.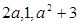 按某种顺序排列成等差数列。
按某种顺序排列成等差数列。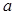 的值;
的值; 的首项、公差都为
的首项、公差都为 的首项、公比也都为
的首项、公比也都为 项和分别为
项和分别为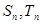 ,且
,且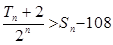 ,求满足条件的正整数
,求满足条件的正整数 为递减的等差数列,
为递减的等差数列,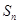 是数列
是数列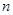 项和,且
项和,且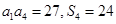 .
.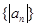 的前
的前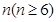 项和
项和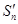
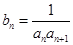 ,求数列
,求数列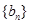 的前
的前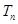
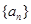 的前6项和为60,且
的前6项和为60,且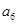 为
为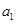 和
和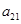 的等比中项.
的等比中项.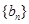 满足
满足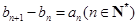 ,且
,且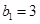 ,求数列
,求数列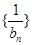 的前
的前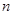 项和
项和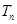 .
.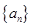 的前
的前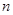 项和为
项和为 ,若
,若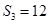 ,且
,且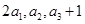 成等比数列.求
成等比数列.求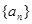 中,
中,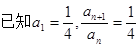 ,
, .求
.求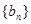 的通项公式.
的通项公式. 的前
的前 项和为
项和为 ,且满足
,且满足 为常数,则称该数列为
为常数,则称该数列为 数列.
数列. 是否为
是否为 且公差不为零的等差数列
且公差不为零的等差数列 满足
满足 ,求
,求 的最小值
的最小值 ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn},