题目内容
(本题满分14分)
若等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 为常数,则称该数列为
为常数,则称该数列为 数列.
数列.
(1)判断 是否为
是否为 数列?并说明理由;
数列?并说明理由;
(2)若首项为 且公差不为零的等差数列
且公差不为零的等差数列 为
为 数列,试求出该数列的通项公式;
数列,试求出该数列的通项公式;
(3)若首项为 ,公差不为零且各项为正数的等差数列
,公差不为零且各项为正数的等差数列 为
为 数列,正整数
数列,正整数 满足
满足 ,求
,求 的最小值
的最小值
(1)它为 数列 ;(2)
数列 ;(2) 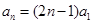 ,其中
,其中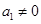 .
.
(3)最小值为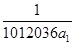 ,当且仅当
,当且仅当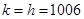 取等号
取等号
解析试题分析:(1)由等差数列的通项公式找出等差数列的首项和公差,然后利用等差数列的前n项和的公式表示出Sn和S2n,求出 等于
等于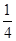 为常数,所以得到该数列为S数列;
为常数,所以得到该数列为S数列;
(2)设此数列的公差为d,根据首项和公差,利用等差数列的前n项和的公式表示出Sn和S2n,因为此数列为S数列,得到  等于常数,设比值等于k,去分母化简后得到关于n的一个多项式等于0,令其系数和常数项等于0即可求出k和d值,根据首项和公差d写出该数列的通项公式即可.
等于常数,设比值等于k,去分母化简后得到关于n的一个多项式等于0,令其系数和常数项等于0即可求出k和d值,根据首项和公差d写出该数列的通项公式即可.
(3)根据已知条件首项为a1的各项为正数的等差数列{an}为S数列,设n+h=2008,利用基本不等式求出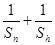 的最小值.
的最小值.
解:(1)由 ,得
,得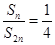 ,所以它为
,所以它为 数列
数列
(2)假设存在等差数列 ,公差为
,公差为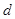 ,则
,则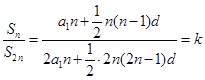 (常数)
(常数)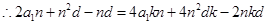 化简得
化简得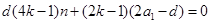 ①
①
由于①对任意正整数 均成立,则
均成立,则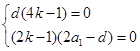
解得: 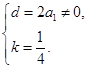 ,故存在符合条件的等差数列.
,故存在符合条件的等差数列.
其通项公式为: 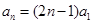 ,其中
,其中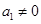 .
.
(3)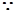
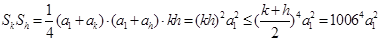
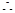
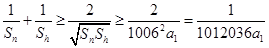
其最小值为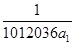 ,当且仅当
,当且仅当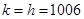 取等号
取等号
考点:本试题主要考查了等差数列和数列求和的问题,是一道综合题。
点评:解决该试题的关键是学生灵活运用等差数列的通项公式及前n项和的公式化简求值,掌握题中的新定义并会利用新定义化简求值。

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ,1,
,1, 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值;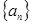 的首项、公差都为
的首项、公差都为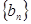 的首项、公比也都为
的首项、公比也都为 项和分别
项和分别 ,且
,且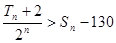 ,求满足条件的正整数
,求满足条件的正整数 中,
中, ,且
,且 、
、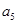 、
、 成等比数列.
成等比数列. ,求数列
,求数列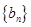 的前
的前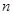 项的和
项的和 .
. 是公差不为零的等差数列,
是公差不为零的等差数列,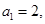 且
且 成等比数列
成等比数列 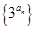 的前
的前 项和
项和  满足:
满足: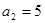 ,
,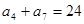 ,
,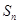 .
.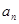 及前n项和
及前n项和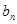 =
=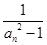 (n
(n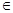 N*),求数列
N*),求数列 的前n项和
的前n项和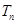 .
.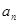 }中,
}中,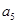 =162,公比q=3,前n项和
=162,公比q=3,前n项和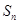 =242,求首项
=242,求首项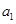 和项数n的值.
和项数n的值.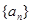 的前n项和,
的前n项和,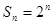 ,求
,求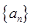 满足:
满足: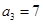 ,
, ,
,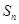 .
.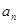 及
及 (
( ),求数列
),求数列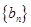 的前n项和
的前n项和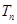 .
.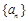 的前n项和为
的前n项和为 ,且
,且 ,
, .
. ,求数列
,求数列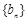 的前n项和
的前n项和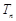 .
. 中,公差
中,公差 又
又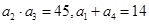 .
. ,数列
,数列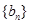 的前
的前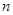 项和记为
项和记为 ,求
,求