题目内容
7.在等腰梯形ABCD中,AD∥BC,AB=AD=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面AECD.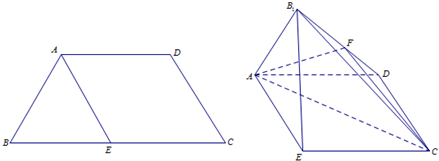
(Ⅰ)若F为B1D的中点,求证:B1E∥平面ACF;
(Ⅱ)求平面ADB1与平面ECB1所成二面角的正弦值.
分析 (Ⅰ)连接ED交AC于O,连接OF,则FO∥B1E,由此能证明B1E∥面ACF.
(Ⅱ)取AE的中点M,分别以ME,MD,MB1为x,y,z轴,建立空间直角坐标系.利用向量法能求出平面ADB1与平面ECB1所成二面角的正弦值.
解答 证明:(Ⅰ)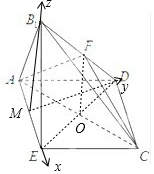 连接ED交AC于O,连接OF,因为AECD为菱形,OE=OD,
连接ED交AC于O,连接OF,因为AECD为菱形,OE=OD,
又F为B1D的中点,所以FO∥B1E,
因为FO?面ACF,B1F?面ACF,
所以B1E∥面ACF.
解:(Ⅱ)取AE的中点M,连接B1M,MD,
分别以ME,MD,MB1为x,y,z轴,建立空间直角坐标系.
A(-$\frac{a}{2}$,0,0),D(0,$\frac{\sqrt{3}}{2}$a,0),B1(0,0,$\frac{\sqrt{3}}{2}a$),E($\frac{a}{2}$,0,0),
C(a,$\frac{\sqrt{3}}{2}$a,0),
$\overrightarrow{AD}$=($\frac{a}{2}$,$\frac{\sqrt{3}a}{2}$,0),$\overrightarrow{A{B}_{1}}$=($\frac{a}{2}$,0,$\frac{\sqrt{3}}{2}a$),
$\overrightarrow{EC}$=($\frac{a}{2},\frac{\sqrt{3}a}{2}$,0),$\overrightarrow{E{B}_{1}}$=(-$\frac{a}{2}$,0,$\frac{\sqrt{3}a}{2}$),
设平面ADB1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=\frac{a}{2}x+\frac{\sqrt{3}a}{2}y=0}\\{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=\frac{a}{2}x+\frac{\sqrt{3}a}{2}z=0}\end{array}\right.$,取a=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3}$,-1,-1),
设平面ECB1的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{EC}=\frac{a}{2}x+\frac{\sqrt{3}a}{2}y=0}\\{\overrightarrow{m}•\overrightarrow{E{B}_{1}}=-\frac{a}{2}x+\frac{\sqrt{3}a}{2}z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3}$,-1,1),
设平面ADB1与平面ECB1所成二面角的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{3}{5}$,∴sin$θ=\frac{4}{5}$.
∴平面ADB1与平面ECB1所成二面角的正弦值为$\frac{4}{5}$.
点评 本题考查线面平行的证明,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.