题目内容
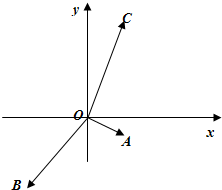 如图,非零向量
如图,非零向量| OA |
| OB |
| π |
| 6 |
| 2π |
| 3 |
| OA |
| OB |
| OC |
| 0 |
| OC |
分析:由题意及图可判断出
与x轴正半轴的夹角的取值范围应在向量-
,-
与x轴正半轴的夹角之间,故由题设中条件非零向量
,
与x轴正半轴的夹角分别为
和
,判断出向量-
,-
与x轴正半轴的夹角范围即可选出正确选项
| OC |
| OA |
| OB |
| OA |
| OB |
| π |
| 6 |
| 2π |
| 3 |
| OA |
| OB |
解答:解:由
+
+
=
得
=-
-
,
即
与x轴正半轴的夹角的取值范围应在向量-
,-
与x轴正半轴的夹角之间,
由于非零向量
,
与x轴正半轴的夹角分别为
和
,
∴向量-
,-
与x轴正半轴的夹角范围是(
,
)
∴
与x轴正半轴的夹角的取值范围是(
,
)
故选B
| OA |
| OB |
| OC |
| 0 |
| OC |
| OA |
| OB |
即
| OC |
| OA |
| OB |
由于非零向量
| OA |
| OB |
| π |
| 6 |
| 2π |
| 3 |
∴向量-
| OA |
| OB |
| π |
| 3 |
| 5π |
| 6 |
∴
| OC |
| π |
| 3 |
| 5π |
| 6 |
故选B
点评:本题考查平面向量的综合运用,考查了向量的夹角,向量的相等等,解题的关键是理解题意,判断出
与x轴正半轴的夹角的取值范围应在向量-
,-
与x轴正半轴的夹角之间,本题借助图形判断考查了数形结合的思想及判断推理的能力.
| OC |
| OA |
| OB |

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
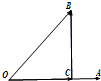 如图,非零向量
如图,非零向量| OA |
| OB |
| BC |
| OA |
| OC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,非零向量
如图,非零向量 如图,非零向量
如图,非零向量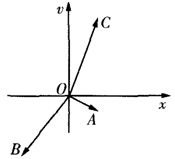 如图,非零向量
如图,非零向量