题目内容
用向量方法证明：对角线互相平分的四边形是平行四边形.已知：如图,四边形ABCD,对角线AC与BD交于点O,且AO＝OC,DO＝OB,
求证：四边形ABCD是平行四边形.
思路分析：要证明四边形是平行四边形只要证明某一组对边平行且相等即可.由相等向量的意义可知,只需证明其一组对边对应的向量是相等向量.
证明：由已知,得
,
.
∵
,且A、D、B、C不在同一直线上.
故四边形ABCD是平行四边形.
方法归纳 用向量加法的三角形法则作两个向量的和时,可以以其中某一向量的终点为起点作第二个向量,则以第一个向量的起点为起点,以第二个向量的终点为终点的向量就表示两个向量的和.
练习册系列答案
相关题目
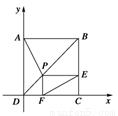
在正方形ABCD中，P是对角线BD上一点，E、F分别在边BC、CD上，且四边形PECF为矩形，用向量方法证明：
