题目内容
17.已知函数f(x)=2sin$\frac{x}{2}$cos$\frac{x}{2}$-2$\sqrt{3}$sin2$\frac{x}{2}$+$\sqrt{3}$(Ⅰ)y=f(x)的图象可由y=sinx的图象经过怎样的变换得到?
(Ⅱ)若y=f(x+φ)的一个对称中心为($\frac{π}{3}$,0),求φ的值;
(Ⅲ)设当x=θ时,函数g(x)=f(x)+sinx取得最大值,求cosθ.
分析 (Ⅰ)利用三角恒等变换化简函数f(x)的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
(Ⅱ)利用正弦函数的图象的对称性,求得φ的值.
(Ⅲ)设当x=θ时,利用辅助角公式,求得g(x)=f(x)+sinx取得最大值时,cosθ的值.
解答 解:(Ⅰ)∵函数f(x)=2sin$\frac{x}{2}$cos$\frac{x}{2}$-2$\sqrt{3}$sin2$\frac{x}{2}$+$\sqrt{3}$=sinx+$\sqrt{3}$cosx=2sin(x+$\frac{π}{3}$),
故把y=sinx的图象向左平移$\frac{π}{3}$个单位,可得y=sin(x+$\frac{π}{3}$)的图象,
再把各点的纵坐标变为原来的2倍,可得f(x)=2sin(x+$\frac{π}{3}$)的图象.
(Ⅱ)若y=f(x+φ)=2sin(x+φ+$\frac{π}{3}$)的一个对称中心为($\frac{π}{3}$,0),
则$\frac{π}{3}$+φ+$\frac{π}{3}$=kπ,k∈Z,∴φ=$\frac{π}{3}$.
(Ⅲ)设当x=θ时,函数g(x)=f(x)+sinx=2sin(θ+$\frac{π}{3}$)+sinθ=2sinθ+$\sqrt{3}$cosθ=$\sqrt{7}$($\frac{2}{\sqrt{7}}$sinθ+$\frac{\sqrt{3}}{\sqrt{7}}$cosθ)
=$\sqrt{7}$sin(θ+arcsin$\frac{\sqrt{3}}{\sqrt{7}}$)取得最大为$\sqrt{7}$,此时,sinθ=$\frac{2}{\sqrt{7}}$,cosθ=$\frac{\sqrt{3}}{\sqrt{7}}$.
点评 本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,辅助角公式的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0 | B. | |$\overrightarrow{AB}$+$\overrightarrow{AC}$|≥2|$\overrightarrow{AD}$| | C. | $\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|2 | D. | $\overrightarrow{AC}$•$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$=|$\overrightarrow{AB}$|sinB |
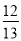 ,cos C=
,cos C=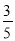 .
.