题目内容
3.在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,AB=BC=1,$CD=\sqrt{7}$,则三棱锥A-BCD的外接球的体积为$\frac{9π}{2}$.分析 取AD的中点O,连结OB、OC.由线面垂直的判定与性质,证出AB⊥BD且AC⊥CD,得到△ABD与△ACD是具有公共斜边的直角三角形,从而得出OA=OB=OC=OD=$\frac{1}{2}$AD,所以A、B、C、D四点在以O为球心的球面上,再根据题中的数据利用勾股定理算出AD长,即可得到三棱锥A-BCD外接球的半径大小.
解答 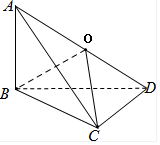 解:取AD的中点O,连结OB、OC
解:取AD的中点O,连结OB、OC
∵AB⊥平面BCD,CD?平面BCD,∴AB⊥CD,
又∵BC⊥CD,AB∩BC=B,∴CD⊥平面ABC,
∵AC?平面ABC,∴CD⊥AC,
∵OC是Rt△ADC的斜边上的中线,OC=$\frac{1}{2}$AD.
同理可得:Rt△ABD中,OB=$\frac{1}{2}$AD,
∴OA=OB=OC=OD=$\frac{1}{2}$AD,可得A、B、C、D四点在以O为球心的球面上.
Rt△ABD中,AB=1且BD=2$\sqrt{2}$,可得AD=3,
由此可得球O的半径R=$\frac{3}{2}$,
∴三棱锥A-BCD的外接球体积为$\frac{4}{3}π•\frac{27}{8}$=$\frac{9π}{2}$.
故答案为:$\frac{9π}{2}$.
点评 本题已知三棱锥的底面为直角三角形,求三棱锥A-BCD的外接球体积.着重考查了线面垂直的判定与性质、勾股定理与球内接多面体等知识,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
13.设x,y满足约束条件$\left\{\begin{array}{l}y-x≤0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$,则z=x-3y的最大值为( )
| A. | 4 | B. | $\frac{3}{2}$ | C. | $-\frac{8}{3}$ | D. | 2 |
14.函数f(x)=(x-1)2的单调递增区间是( )
| A. | [0,+∞) | B. | [1,+∞) | C. | (-∞,0] | D. | (-∞,1] |
18.南北朝时期的数学家祖冲之,利用“割圆术”得出圆周率π的值在3.1415926与3.1415927之间,成为世界上第一把圆周率的值精确到7位小数的人,他的这项伟大成就比外国数学家得出这样精确数值的时间,至少要早一千年,创造了当时世界上的最高水平.我们用概率模型方法估算圆周率,向正方形及其内切圆随机投掷豆子,在正方形中的80颗豆子中,落在圆内的有64颗,则估算圆周率的值为( )
| A. | 3.1 | B. | 3.14 | C. | 3.15 | D. | 3.2 |
8.已知集合A={x|x2-2x-3≤0},B={y|y=2x},则A∩B=( )
| A. | (0,3] | B. | (0,3) | C. | [0,3] | D. | [3,+∞) |