题目内容
7.某调研机构调取了当地2014年10月~2015年3月每月的雾霾天数与严重交通事故案例数资料进行数据统计分析,以备下一年如何预防严重交通事故作参考,部分资料如下:| 时间 | 14年10月 | 14年11月 | 14年12月 | 15年1月 | 15年2月 | 15年3月 |
| 雾霾天数 | 7 | 11 | 13 | 12 | 10 | 8 |
| 严重交通事故案例数 | 14 | 25 | 29 | 26 | 22 | 16 |
(1)求剔除的2组数据不是相邻2个月数据的概率;
(2)若剔除的是2014年10月与2015年2月这两组数据,请你根据其它4个月的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)①根据(2)所求的回归方程,求2014年10月与2015年2月的严重交通事故案例数;
②判断(2)所求的线性回归方程是否是合情的.
[附:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}xy-x\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\overline{a}$=$\overrightarrow{y}$-b$\overrightarrow{x}$].
分析 (1)本题是一个古典概型,确定试验发生包含的事件、满足条件的事件的种数,根据古典概型的概率公式得到结果.
(2)根据所给的数据,求出x,y的平均数,根据求线性回归方程系数的方法,求出系数b,把b和x,y的平均数,代入求a的公式,做出a的值,写出线性回归方程.
(3)根据所求的线性回归方程,预报当自变量为10和7时的y的值,把预报的值同原来表中所给的10和7对应的值做差,差的绝对值不超过2,得到线性回归方程理想
解答 解:(1)设抽到不相邻两个月的数据为事件A,
∵从6组数据中选取2组数据共有${C}_{6}^{2}$=15种情况,每种情况是等可能出现的,
其中抽到相邻两个月的数据的情况有5种,
故A事件共包含10种不同的情况,
∴P(A)=$\frac{10}{15}$=$\frac{2}{3}$;
(2)由数据求得:$\overline{x}$=11,$\overline{y}$=24,
由公式求得$\hat{b}$=$\frac{18}{7}$,由$\hat{a}$=$\overline{y}$-$\hat{b}$$\overline{x}$=-$\frac{30}{7}$,
∴y关于x的线性回归方程为:$\hat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$,
(3)①当x=7时,$\hat{y}$=$\frac{96}{7}$,
同样,当x=10时,$\hat{y}$=$\frac{150}{7}$,
②∵|$\frac{96}{7}$-14|=$\frac{2}{7}$<2,
|$\frac{150}{7}$-22|=$\frac{4}{7}$<2,
所以该线性回归方程是合情的.
点评 本题考查线性回归方程的求法,考查等可能事件的概率,考查线性分析的应用,考查解决实际问题的能力,是一个综合题目.

 名校课堂系列答案
名校课堂系列答案| A. | ($\frac{1}{2}$,1) | B. | (1,+∞) | C. | (-∞,1) | D. | [1,+∞) |
| A. | 互斥但非对立事件 | B. | 对立事件 | ||
| C. | 相互独立事件 | D. | 以上都不对 |
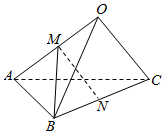 已知三棱锥O-ABC,OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M,N分别是棱OA,BC的中点.求:直线MN与AC所成的角余弦值.
已知三棱锥O-ABC,OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M,N分别是棱OA,BC的中点.求:直线MN与AC所成的角余弦值.