题目内容
15.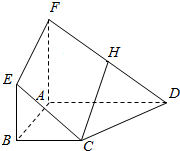 如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.
如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.(1)证明:CH∥平面ABEF;
(2)判断C、D、E、F四点是否共面,并说明理由.
分析 (Ⅰ)取FA中点G,连HG,BG,由已知得四边形BCHG是平行四边形,由此能证明CH∥平面ABEF.
(Ⅱ)由已知推导出EF∥BG,EF∥CH,由此结合已知条件能证明C,D,F,E四点共面.
解答 (Ⅰ)证明:取FA中点G,连HG,BG,
∵FG=GA,FH=HD∴GH$\underline{\underline{∥}}$$\frac{1}{2}AD$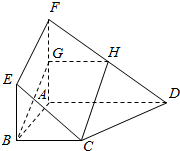
又BC$\underline{\underline{∥}}$$\frac{1}{2}AD$,故GH$\underline{\underline{∥}}$BC
∴四边形BCHG是平行四边形.∴CH∥BG
又BG?平面ABEF,CH?平面ABEF,
∴CH∥平面ABEF,(6分)
(Ⅱ)解:C,D,F,E四点共面.理由如下:(8分)
由BE$\underline{\underline{∥}}$$\frac{1}{2}AF$,G是FA的中点知,BE$\underline{\underline{∥}}$GF,∴EF∥BG
由(Ⅰ)知BG∥CH,∴EF∥CH,
故EC,FH共面.又点D在直线FH上
∴C,D,F,E四点共面.(12分)
点评 本题考查线面平行的证明,考查四点共面的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
17.y=$\frac{sinx}{|sinx|}-\frac{cosx}{|cosx|}$(x∈R,且x≠$\frac{kπ}{2}$,k∈Z)的值域是( )
| A. | [-2,2] | B. | {-2,2} | C. | {0,2} | D. | {-2,0,2} |
20.已知函数y=f(1-x2)的定义域[-2,3],则函数g(x)=$\frac{f(2x+1)}{x+2}$的定义域是( )
| A. | (-∞,-2)∪(-2,3] | B. | [-8,-2)∪(-2,1] | C. | [-$\frac{9}{2}$,-2)∪(-2,0] | D. | [-$\frac{9}{2}$,-2] |
5.若a<b<0,则下列结论不正确的是( )
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | $\frac{a-b}{a}$>0 | C. | a2<b2 | D. | a3<b3 |
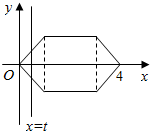 如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6
如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6