题目内容
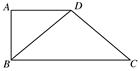
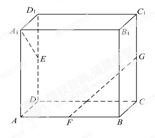
如图,在矩形 中,点
中,点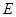 为边
为边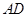 上的点,点
上的点,点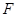 为边
为边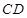 的中点,
的中点,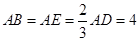 ,现将
,现将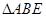 沿
沿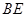 边折至
边折至 位置,且平面
位置,且平面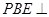 平面
平面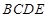 .
.
(1) 求证:平面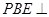 平面
平面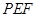 ;
;
(2) 求四棱锥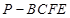 的体积.
的体积.
 中,点
中,点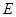 为边
为边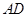 上的点,点
上的点,点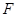 为边
为边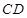 的中点,
的中点,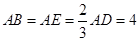 ,现将
,现将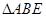 沿
沿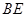 边折至
边折至 位置,且平面
位置,且平面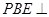 平面
平面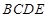 .
.
(1) 求证:平面
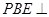 平面
平面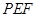 ;
;(2) 求四棱锥
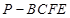 的体积.
的体积.(1)详见解析;(2) .
.
 .
.试题分析:(1) 利用直角三角形,先证明折前有
 ,折后这个垂直关系没有改变,然后由平面
,折后这个垂直关系没有改变,然后由平面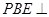 平面
平面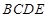 的性质证明
的性质证明 平面
平面 ,最后由面面垂直的判定定理即可证明平面
,最后由面面垂直的判定定理即可证明平面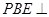 平面
平面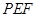 ;(2)由
;(2)由 ,可求出体积为
,可求出体积为 .
.试题解析:(1) 证明:由题可知:折前
 ,这个垂直关系,折后没有改变
,这个垂直关系,折后没有改变故折后有

(2)由题意四棱锥
 的高
的高

 10分
10分则
 12分.
12分.
练习册系列答案
相关题目
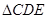 中
中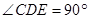 ,平面
,平面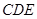 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB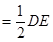 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
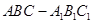 中,点
中,点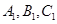 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且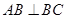 ,
,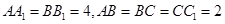 ,E为
,E为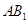 中点,
中点,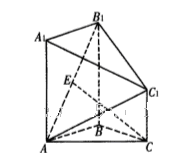
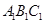 ,
,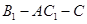 的大小.
的大小.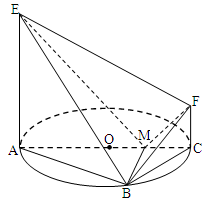
 中,点
中,点 是
是 的中点,
的中点,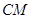 和
和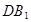 所成角的余弦值为( )
所成角的余弦值为( )







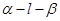 的棱
的棱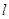 上的两点,分别在
上的两点,分别在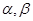 内作垂直于棱
内作垂直于棱 D.
D.