题目内容
已知函数![]()
(1)若f(x)在[1,+∞)上单调递增,求a的取值范围;
(2)若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1、x2总有以下不等式![]() 成立,则称函数y=f(x)为区间D上的“凹函数”.试判断当a≤0时,f(x)是否为“凹函数”,并对你的判断加以证明.
成立,则称函数y=f(x)为区间D上的“凹函数”.试判断当a≤0时,f(x)是否为“凹函数”,并对你的判断加以证明.
答案:
解析:
解析:
|
(Ⅰ)由 欲使函数为[1,+∞)上单调增函数,则 令 (Ⅱ)证明:由 而 又 ∵ ∵ 由①、②、③得 即 从而由凹函数的定义可知函数为凹函数. 14分 |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
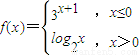 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .