题目内容

设实数a、b满足
3a-2b+1≥0
3a+2b-4≥0
a≤1
，则9a2+4b2的最大值是
25
25
．
分析：本题考查的知识点是简单线性规划的应用，我们要先画出满足约束条件
3a-2b+1≥0
3a+2b-4≥0
a≤1
的平面区域，然后分析平面区域里各个角点，然后将其代入9a2+4b2中，求出9a2+4b2的最大值
解答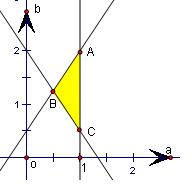：解：满足约束条件
3a-2b+1≥0
3a+2b-4≥0
a≤1
的平面区域如下图示：
由图可知，当a=1，b=2时，
9a2+4b2有最大值25
故答案为：25．
点评：平面区域的最值问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，分析表达式的几何意义，然后结合数形结合的思想，分析图形，找出满足条件的点的坐标，即可求出答案．
练习册系列答案
相关题目
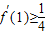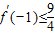设函数f（x）=Ax3+Bx2+Cx+6A+B，其中实数A，B，C满足：①-8B+1≤12A+4C≤8B+9，②3A＜-B≤6A
（Ⅰ）求证：f′(1)≥
1
4
；f′(-1)≤
9
4
；
（Ⅱ）设0≤x≤π，求证：f（2sinx）≥0．
设函数f(x)=
cos(πx-π)+1  x∈(
1
2
，1) ∪(1，
3
2
)
a                      x=1
，若关于x的方程2[f（x）]2-（2a+3）f（x）+3a=0有五个不同的实数解，则满足题意的a的取值范围是 （　　）
已知A（-2，4），B（3，-1），C（-3，-4）．设
AB
=
a
，
BC
=
b
，
CA
=
c
，且
CM
=3 
c
，
CN
=-2
b
．
（1）求3
a
+
b
-3
c
；
（2）求满足
a
=m
b
+n
c
的实数m，n．
设函数f（x）=Ax3+Bx2+Cx+6A+B，其中实数A，B，C满足：①-8B+1≤12A+4C≤8B+9，②3A＜-B≤6A
（Ⅰ）求证：；；
（Ⅱ）设0≤x≤π，求证：f（2sinx）≥0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网