题目内容
设a,b,c是实数,那么对任何实数x,不等式asinx+bcosx+c>0都成立的充要条件是( )
| A.a,b同时为0,且c>0 | B.
| ||||
C.
| D.
|
asinx+bcosx+c=
sin(x+φ)+c>0对任何实数x恒成立,
而
sin(x+φ)+c的最小值为c-
∴c-
>0即
<c
故选C.
| a2+b2 |
而
| a2+b2 |
| a2+b2 |
∴c-
| a2+b2 |
| a2+b2 |
故选C.

练习册系列答案
相关题目
 =c
=c <c
<c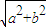 >c
>c