题目内容
设a,b,c是实数,那么对任何实数x,不等式asinx+bcosx+c>0都成立的充要条件是( )
分析:根据asinx+bcosx=
sin(x+φ),求出asinx+bcosx+c的最小值,使最小值大于0,即可得到结论.
| a2+b2 |
解答:解:asinx+bcosx+c=
sin(x+φ)+c>0对任何实数x恒成立,
而
sin(x+φ)+c的最小值为c-
∴c-
>0即
<c
故选C.
| a2+b2 |
而
| a2+b2 |
| a2+b2 |
∴c-
| a2+b2 |
| a2+b2 |
故选C.
点评:本题主要考查了必要条件、充分条件与充要条件的判断,以及三角函数的最值,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
 =c
=c <c
<c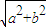 >c
>c