题目内容
已知函数 在
在 与
与 时都取得极值
时都取得极值
(1)求 的值与函数
的值与函数 的单调区间
的单调区间
(2)若 ,且对
,且对 ,不等式
,不等式 恒成立,求m的取值范围.
恒成立,求m的取值范围.
(1)  函数
函数 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是
(2)
【解析】
试题分析:根据函数在某点取得极值,得到对应的导数等于 0,得出相应的方程组,从而求出所求参数的值,根据 ,进一步确定出函数的解析式,由不等式恒成立,得出函数
,进一步确定出函数的解析式,由不等式恒成立,得出函数 在
在 时的最大值满足条件即可,从而将问题转化为函数在某个闭区间上的最值问题来解决.
时的最大值满足条件即可,从而将问题转化为函数在某个闭区间上的最值问题来解决.
试题解析:(1)
由 ,
, 得
得 2分
2分
 ,令
,令 3分
3分
当x变化时, 变化如下表:
变化如下表:
|
|
|
|
|
|
| |
|
| | |
| 极大值 | 极小值 |
5分
所以函数 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是 ; 6分
; 6分
(2) ,
, 8分
8分
当 时,
时, 为极大值. 而
为极大值. 而 ,则
,则 为最大值, 10分
为最大值, 10分
要使 恒成立,则只需要
恒成立,则只需要 ,
,
得 ∴实数m的取值范围为
∴实数m的取值范围为 12分
12分
考点:函数的极值点,函数在某个闭区间上的最值,不等式恒成立.

练习册系列答案
相关题目







 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为 ,斜率为
,斜率为 的直线
的直线 交y轴于点
交y轴于点 .
.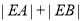 .
. 的值域为R,那么a的取值范围是( )
的值域为R,那么a的取值范围是( ) B.
B. C.
C. D.
D.
 的零点所在的区间为( )
的零点所在的区间为( ) B.
B. C.
C. D.
D.
 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 弦被点A(1,1)平分,那么这条弦所在的直线方程是 ;
弦被点A(1,1)平分,那么这条弦所在的直线方程是 ; ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;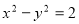 绕原点逆时针转动
绕原点逆时针转动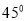 ,就会得到它的一条“共性双曲线”
,就会得到它的一条“共性双曲线”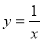 ;根据以上材料可推理得出双曲线
;根据以上材料可推理得出双曲线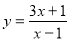 的焦距为( )
的焦距为( )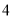 B.
B.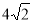 C.
C.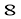 D.
D.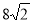
 分别是与
分别是与 轴正方向同向的单位向量,平面内三点A、B、C满足,
轴正方向同向的单位向量,平面内三点A、B、C满足, ,
, .若A、B、C三点构成直角三角形,则实数m的值为 .
.若A、B、C三点构成直角三角形,则实数m的值为 .