题目内容
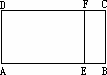
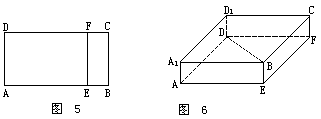
有一矩形纸片ABCD，按图所示方法进行任意折叠，使每次折叠后点B都落在边AD上，将B的落点记为B′，其中EF为折痕，点F也可落在边CD上，过B′作B′H∥CD交EF于点H，则点H的轨迹为（ ）
A．圆的一部分
B．椭圆的一部分
C．双曲线的一部分
D．抛物线的一部分
【答案】分析：根据折纸的方法可知，点H到定点B的距离以及到定直线AD的距离相等，根据抛物线的定义可知答案．
解答：解：由题意知：点H到定点B的距离以及到定直线AD的距离相等，
根据抛物线的定义可知：
点H的轨迹为：抛物线，（抛物线的一部分）
故选D．
点评：本题主要考查了抛物线的定义，解题的关键是找出点H的特征，即它到定点B的距离以及到定直线AD的距离相等，属于基础题．
解答：解：由题意知：点H到定点B的距离以及到定直线AD的距离相等，
根据抛物线的定义可知：
点H的轨迹为：抛物线，（抛物线的一部分）
故选D．
点评：本题主要考查了抛物线的定义，解题的关键是找出点H的特征，即它到定点B的距离以及到定直线AD的距离相等，属于基础题．
练习册系列答案
相关题目
9、有一矩形纸片ABCD，按图所示方法进行任意折叠，使每次折叠后点B都落在边AD上，将B的落点记为B′，其中EF为折痕，点F也可落在边CD上，过B′作B′H∥CD交EF于点H，则点H的轨迹为（ ）
