题目内容
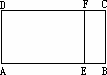
有一矩形纸片ABCD，AB=5，BC=2，E，F分别是AB，CD上的点，且BE=CF=1，把纸片沿EF折成直二面角．
（1）求BD的距离；
（2）求证AC，BD交于一点且被这点平分．
|
解析:
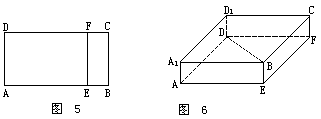
将平面BF折起后所补形成长方体AEFD-A1BCD1，
则BD恰好是长方体的一条对角线．
（1）解：因为AE，EF，EB两两垂直，
所以BD恰好是以AE，EF，EB为长、宽、高的
长方体的对角线，
．．．．．．．．．．．．．．．．6分
（2）证明：因为AD 
EF，EF BC，所以AD BC．
所以ACBD在同一平面内，
且四边形ABCD为平行四边形．
所以AC、BD交于一点且被这点平分
练习册系列答案
相关题目
9、有一矩形纸片ABCD，按图所示方法进行任意折叠，使每次折叠后点B都落在边AD上，将B的落点记为B′，其中EF为折痕，点F也可落在边CD上，过B′作B′H∥CD交EF于点H，则点H的轨迹为（ ）
