题目内容

16．已知函数f（x）=loga（x-1）-2（a＞0且a≠1），则函数恒过定点（2，-2）．

分析 根据对数函数的恒过点性质求解．

解答 解：根据对数函数的恒过点性质：
可得：x-1=1，
解得：x=2．
那么：y=）=loga1-2=-2．
则函数恒过定点为（2，-2）．
故答案为（2，-2）．

点评 本题考查了对数函数的恒过点性质．比较基础．

练习册系列答案
相关题目
6．已知向量$\overrightarrow{AB}$=（1，5，-2），$\overrightarrow{BC}$=（3，1，2），$\overrightarrow{DE}$=（x，-3，6）．若DE∥平面ABC，则x的值是（　　）
A．5B．3C．2D．-1
7．函数y=$\frac{x+4}{\sqrt{x}}$的定义域是（0，+∞）；最小值是4．
4．已知f（x）=x2+mx+1（m∈R），g（x）=ex．
（1）当x∈[0，2]时，F（x）=f（x）-g（x）为增函数，求实数m的取值范围；
（2）若m∈（-1，0），设函数$G（x）=\frac{f（x）}{g（x）}，H（x）=-\frac{1}{4}x+\frac{5}{4}$，求证：对任意x1，x2∈[1，1-m]，G（x1）＜H（x2）恒成立．
11．已知α是第二象限角，且sinα=$\frac{3}{5}$，则cos（π-α）=（　　）
A．$\frac{4}{5}$B．-$\frac{4}{5}$C．$\frac{3}{5}$D．-$\frac{3}{5}$
1．已知函数f（x）=$\frac{{2}^{x}}{{2}^{x}+1}$+t，t∈R．
（Ⅰ）如果函数f（x）是R上的奇函数，求实数t的值．
（Ⅱ）判断f（x）在R上的单调性，并用定义证明你的结论．
8．在△ABC中，已知sinA：sinB：sinC=3：5：7，则此三角形的最小内角的余弦值等于$\frac{13}{14}$．
14．设数列{an}（n≥1，n∈N）满足a1=2，a2=6，且an+2-2an+1+an=2，若[x]表示不超过x的最大整数，则$[{\frac{2017}{a_1}+\frac{2017}{a_2}+…+\frac{2017}{{{a_{2017}}}}}]$=2016．
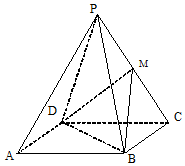15．已知四棱锥P-ABCD中底面四边形ABCD是正方形，各侧面都是边长为2的正三角形，M是棱PC的中点．建立空间直角坐标系，利用空间向量方法解答以下问题：
（1）求证：PA∥平面BMD；
（2）求二面角M-BD-C的平面角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网