题目内容
【题目】把函数
的图象向右平移
个单位长度，再把所得的函数图象上所有点的横坐标缩短到原来的
（纵坐标不变）得到函数
的图象，关于的说法有：①函数的图象关于点
对称；②函数的图象的一条对称轴是
；③函数在
上的最上的最小值为
；④函数
上单调递增，则以上说法正确的个数是（ ）
A.4个B.3个C.2个D.1个
【答案】C
【解析】
通过平移变换与伸缩变换求得函数
的解析式.由
判断①错误；由
求得最小值判断②正确；由x的范围求得函数值域判断③正确；由x的范围可知函数在
上不单调判断④错误.
把函数
的图象向右平移
个单位长度，得
，
再把所得的函数图象上所有点的横坐标缩短到原来的
（纵坐标不变）得到函数的图象，
则
.
①∵
，∴函数的图象不关于点
对称，故①错误；
②∵
，∴函数的图象的一条对称轴是
，故②正确；
③当
时，
，则
，即函数在
上的最上的最小值为
，故③正确；
④当
时，
，可知函数在上不单调，故④错误.
∴正确命题的个数为2.
故选：C.
【题目】某省确定从2021年开始，高考采用“
”的模式，取消文理分科，即“3”包括语文、数学、外语，为必考科目；“1”表示从物理、历史中任选一门；“2”则是从生物、化学、地理、政治中选择两门，共计六门考试科目.某高中从高一年级2000名学生（其中女生900人）中，采用分层抽样的方法抽取
名学生进行调查.
（1）已知抽取的名学生中含男生110人，求的值及抽取到的女生人数；
（2）学校计划在高二上学期开设选修中的“物理”和“历史”两个科目，为了了解学生对这两个科目的选课情况，对在（1）的条件下抽取到的名学生进行问卷调杳（假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目）.下表是根据调查结果得到的
列联表，请将列联表补充完整，并判断是否有
的把握认为选择科目与性别有关？说明你的理由；
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
（3）在（2）的条件下，从抽取的选择“物理”的学生中按分层抽样抽取6人，再从这6名学生中抽取2人，对“物理”的选课意向作深入了解，求2人中至少有1名女生的概率.
附：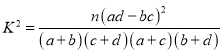
，其中
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】万众瞩目的第14届全国冬季运动运会（简称“十四冬”）于2020年2月16日在呼伦贝尔市盛大开幕，期间正值我市学校放寒假，寒假结束后，某校工会对全校100名教职工在“十四冬”期间每天收看比赛转播的时间作了一次调查，得到如图频数分布直方图：
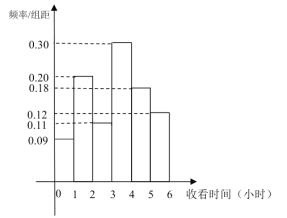
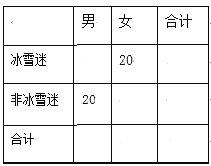
（1）若将每天收看比赛转播时间不低于3小时的教职工定义为“冰雪迷”，否则定义为“非冰雪迷”，请根据频率分布直方图补全
列联表；并判断能否有
的把握认为该校教职工是否为“冰雪迷”与“性别”有关；
（2）在全校“冰雪迷”中按性别分层抽样抽取6名，再从这6名“冰雪迷”中选取2名作冰雪运动知识讲座.记其中女职工的人数为
，求的分布列与数学期望.
附表及公式：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，
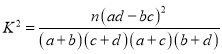