题目内容
【题目】如图,在四面体ABCD中,AC=6,BA=BC=5,AD=CD=3![]() .
.
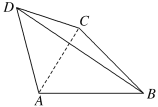
(1)求证:AC⊥BD;
(2)当四面体ABCD的体积最大时,求点A到平面BCD的距离.
【答案】(1)见解析(2)![]()
【解析】
(1)取AC的中点O,连接OB与OD,证明AC⊥平面OBD,即可得证;
(2)当四面体ABCD的体积最大时,平面DAC⊥平面ABC,利用等体积法求解点到平面距离.
(1)证明:

如图,取AC的中点O,连接OB与OD,∵BA=BC,
∴AC⊥OB ∵AD=CD,∴AC⊥OD,又OD∩OB=O,
∴AC⊥平面OBD,又BD平面OBD,∴AC⊥BD.
(2)由题可知,当四面体ABCD的体积最大时,平面DAC⊥平面ABC,∵DO⊥AC,
∴DO⊥平面ABC,又OB平面ABC,∴DO⊥OB,
∵DA=DC=3![]() ,AC=6,AB=BC=5,∴OD=
,AC=6,AB=BC=5,∴OD=![]() =
=![]() =3,
=3,
OB=![]() =
=![]() =4,∴DB=
=4,∴DB=![]() =
=![]() =5,
=5,
又BC=5,
∴在△BCD中,CD边上的高h= =
=![]() =
=![]() ,
,
∴S△BCD=![]() ×CD×h=
×CD×h=![]() ×3
×3![]() ×
×![]() =
=![]() ,S△ABC=
,S△ABC=![]() ×AC×OB=
×AC×OB=![]() ×6×4=12.
×6×4=12.
设点A到平面BCD的距离为d,∴VABCD=VDABC,即![]() S△BCD×d=
S△BCD×d=![]() S△ABC×OD,
S△ABC×OD,
∴d=![]() =
=![]() =
=![]() ,∴点A到平面BCD的距离为
,∴点A到平面BCD的距离为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目