题目内容
对于（0，3）上的一切实数x，不等式（x-2）m＜2x-1恒成立，求实数m的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用
分析：将不等式化为（m-2）x-2m+1＜0，讨论m=2与m≠2的情况，特别是第二种情况，构造一次函数f（x）=（m-2）x-2m+1，根据一次函数的单调性可以将不等式（x-2）m＜2x-1恒成立等价于
，求解即可．
|
解答：
解：不等式（x-2）m＜2x-1可化为，
（m-2）x-2m+1＜0，
当m=2时，不等式显然成立；
当m≠2时，
令f（x）=（m-2）x-2m+1，
则f（x）可看做关于x的一次函数，
对于（0，3）上的一切实数x，不等式（x-2）m＜2x-1恒成立等价于：
，
即
，
解得，
≤m≤5，且m≠2．
综上，实数m的取值范围是[
，5]．
（m-2）x-2m+1＜0，
当m=2时，不等式显然成立；
当m≠2时，
令f（x）=（m-2）x-2m+1，
则f（x）可看做关于x的一次函数，
对于（0，3）上的一切实数x，不等式（x-2）m＜2x-1恒成立等价于：
|
即
|
解得，
| 1 |
| 2 |
综上，实数m的取值范围是[
| 1 |
| 2 |
点评：本题考查不等式的性质，函数与不等式的关系，以及利用函数性质解决不等式恒成立的技巧，属于中档题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
正四面体ABCD的棱长为1，其中线段AB∥平面α，E，F分别是线段AD和BC的中点，当正四面体绕以AB为轴旋转时，线段EF在平面α上的射影E1F1长的范围是（ ）
A、[0，
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
若向量
=（1，2），
=（4，5），则
=（ ）
| BA |
| CA |
| BC |
| A、（5，7） |
| B、（-3，-3） |
| C、（3，3） |
| D、（-5，-7） |
若
=（x，3），
=（3，1）且
∥
，则x的值是（ ）
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
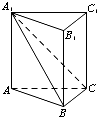如图，在直三棱柱ABC-A1B1C1中，平面A1BC⊥侧面A1ABB1．
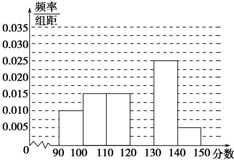某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：