题目内容
已知cos(
+θ)=
,且
+θ∈(-
,0),求
的值.
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| π |
| 2 |
| sin2θ+2sin2θ |
| 1-tanθ |
考点:两角和与差的余弦函数,同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:根据已知,先求出sin2θ,cos2θ,tanθ的值,化简原式后代入即可求值.
解答:
解:cos(
+θ)=
,
⇒
(cosθ-sinθ)=
,
⇒cosθ-sinθ=
,
⇒1-sin2θ=
,
⇒sin2θ=
,
∵
+θ∈(-
,0),∴-
<θ<-
,-
<2θ<-
,
∴cos2θ=-
=-
=
,
∴tanθ=7,(∵sin2θ=
=
,检验后舍去-7),
∴
=
=
=-
.
| π |
| 4 |
| 3 |
| 5 |
⇒
| ||
| 2 |
| 3 |
| 5 |
⇒cosθ-sinθ=
3
| ||
| 5 |
⇒1-sin2θ=
| 18 |
| 25 |
⇒sin2θ=
| 7 |
| 25 |
∵
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 2 |
∴cos2θ=-
| 1-sin22θ |
| 24 |
| 25 |
| 1-tan2θ |
| 1+tan2θ |
∴tanθ=7,(∵sin2θ=
| 7 |
| 25 |
| 2tanθ |
| 1+tan2θ |
∴
| sin2θ+2sin2θ |
| 1-tanθ |
| sin2θ+1-cos2θ |
| 1-tanθ |
| ||||
| 1-7 |
| 28 |
| 125 |
点评:本题主要考察了两角和与差的余弦函数公式的应用,同角三角函数基本关系的运用,其中求tanθ是难点,属于基本知识的考查.

练习册系列答案
相关题目
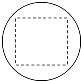 已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、4π | B、8π |
| C、12π | D、16π |
某人午休醒来,发觉表停了,他打开收音机想收听电台整点报时,则他等待的时间短于5分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|