题目内容
函数y=f(x)在点(x0,y0)处的切线方程y=2x+1,则 等于
等于
- A.-4
- B.-2
- C.2
- D.4
D
分析:根据导数几何意义得f′(x0)=2,由导数的定义知f′(x0)= ,由此配出分母上的数字2能够求出
,由此配出分母上的数字2能够求出  的值.
的值.
解答:∵f′(x0)=2,
f′(x0)= =2
=2
∴ =2
=2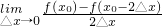 =4
=4
故选D.
点评:本题考查导数的概念和极限的运算,解题时要认真审题,解题的关键是凑出符合导数定义的极限形式,属于基础题.
分析:根据导数几何意义得f′(x0)=2,由导数的定义知f′(x0)=
 ,由此配出分母上的数字2能够求出
,由此配出分母上的数字2能够求出  的值.
的值.解答:∵f′(x0)=2,
f′(x0)=
 =2
=2∴
 =2
=2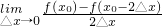 =4
=4故选D.
点评:本题考查导数的概念和极限的运算,解题时要认真审题,解题的关键是凑出符合导数定义的极限形式,属于基础题.

练习册系列答案
相关题目
 函数
函数