题目内容
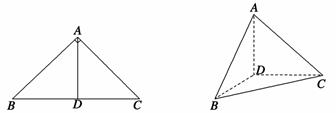
如图,在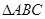 中,
中,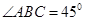 ,
,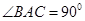 ,
,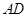 是
是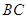 上的高,沿
上的高,沿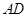 把
把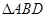 折起,使
折起,使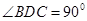 .
.
(Ⅰ)证明:平面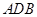 ⊥平面
⊥平面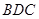 ;
;
(Ⅱ)若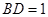 ,求三棱锥
,求三棱锥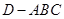 的表面积.
的表面积.
 中,
中, ,
, ,
,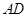 是
是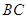 上的高,沿
上的高,沿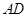 把
把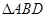 折起,使
折起,使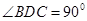 .
.(Ⅰ)证明:平面
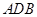 ⊥平面
⊥平面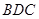 ;
;(Ⅱ)若
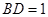 ,求三棱锥
,求三棱锥 的表面积.
的表面积.
(Ⅰ)证明详见解析;(Ⅱ) 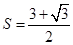 .
.
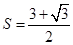 .
.试题分析:(Ⅰ)先证线面垂直
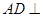 平面
平面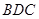 ,再证明面面垂直平面
,再证明面面垂直平面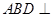 平面
平面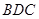 ;(Ⅱ)由第一问可知
;(Ⅱ)由第一问可知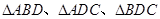 都是直角三角形,可以求出
都是直角三角形,可以求出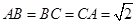 ,所以
,所以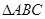 是等边三角形,分别求出四个三角形的面积.
是等边三角形,分别求出四个三角形的面积.试题解析:(Ⅰ)因为折起前
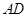 是
是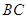 边上的高.
边上的高.所以当
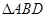 折起后,
折起后,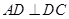 ,
,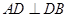 , 3分
, 3分又
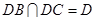 ,所以
,所以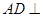 平面
平面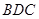 ,因为
,因为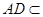 平面
平面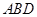 ,
,所以平面
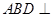 平面
平面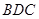 . 6分
. 6分(Ⅱ)由(1)知,
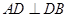 ,
,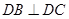 ,
,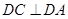 ,
,因为
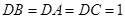 ,
,所以
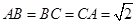 , 9分
, 9分从而
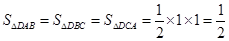 ,
,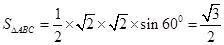 ,
,所以三棱锥
 的表面积
的表面积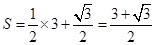 . 12分
. 12分
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 中,
中,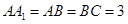 ,
,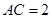 ,
,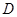 是
是 的中点.
的中点.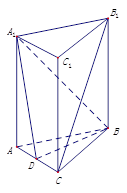
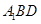 平面
平面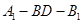 的余弦值.
的余弦值.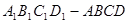 中,
中,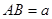 ,
,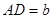 ,
,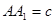 ,
,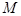 是线段
是线段 的中点.
的中点. 平面
平面 ;
;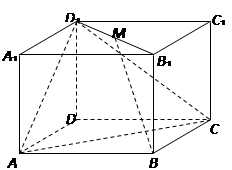
 ,
, ,AD=AB=1,AC和BD交于O点.
,AD=AB=1,AC和BD交于O点.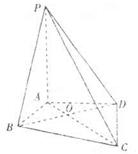
 中,
中,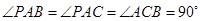 .
.
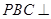 平面
平面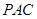 ;
;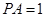 ,
,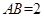 ,当三棱锥
,当三棱锥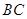 的长.
的长.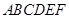 中,四边形
中,四边形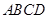 是边长为
是边长为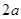 的正方形,平面
的正方形,平面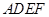 垂直于平面
垂直于平面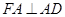 ,
,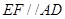 ,
,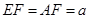 .
.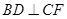 ;
;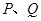 分别为棱
分别为棱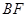 和
和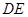 的中点,求证:
的中点,求证: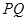 ∥平面
∥平面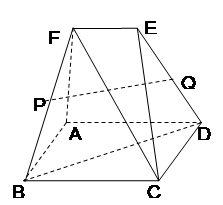
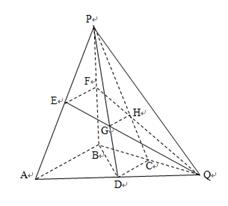
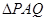 中,
中,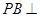 平面
平面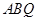 ,
,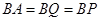 ,
,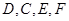 分别是
分别是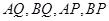 的中点,
的中点,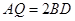 ,
,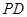 与
与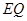 交于
交于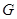 ,
,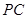 与
与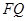 交于点
交于点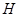 ,连接
,连接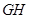 。
。
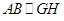 ;
; 的余弦值。
的余弦值。 是平面图形
是平面图形 的直观图,则
的直观图,则
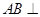 平面
平面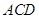 ,
,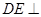 平面
平面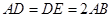 ,
,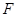 为
为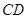 的中点.
的中点.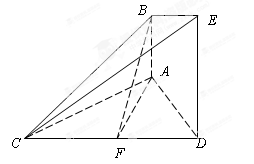
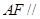 平面
平面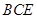 ;
;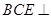 平面
平面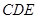 ;
;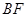 和平面
和平面