题目内容
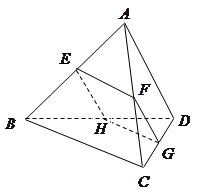
如图,在直三棱柱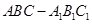 中,
中,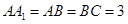 ,
,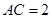 ,
,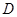 是
是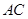 的中点.
的中点.
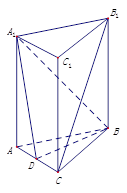
(Ⅰ)求证: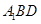 平面
平面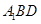 ;
;
(Ⅱ)求二面角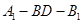 的余弦值.
的余弦值.
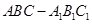 中,
中,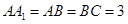 ,
,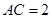 ,
,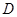 是
是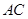 的中点.
的中点.
(Ⅰ)求证:
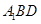 平面
平面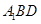 ;
;(Ⅱ)求二面角
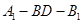 的余弦值.
的余弦值.(Ⅰ)详见解析;(Ⅱ)

试题分析:(Ⅰ)证明线面平行常用以下两种方法:一是用线面平行的判定定理,二是用面面平行的性质.本题用这两种方法都行;
(Ⅱ)首先应考虑作出平面
 截三棱柱所得的截面.作出该截面便很容易得到二面角的平面角即为
截三棱柱所得的截面.作出该截面便很容易得到二面角的平面角即为 .
.本题也可用向量解决.
试题解析:(Ⅰ)法一:连结
 ,交
,交 于
于 ,连结
,连结 ,则
,则 ,从而
,从而 平面
平面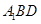 .
.


法二:取
 的中点
的中点 ,连结
,连结 ,易得平面
,易得平面
 ,从而
,从而 平面
平面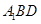 .
.(Ⅱ)
 的中点
的中点 ,连结
,连结 、
、 ,易得平面
,易得平面 就是平面
就是平面 ,
,又
 平面
平面 ,所以
,所以 ,所以
,所以 就是该二面角的平面角.
就是该二面角的平面角. .
.
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
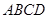 中
中 ,
,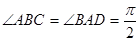 ,
,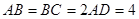 ,
,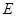 、
、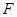 分别是
分别是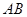 、
、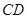 上的点,
上的点,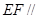
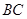 ,
,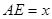 .沿
.沿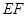 将梯形
将梯形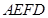 翻折,使平面
翻折,使平面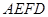 ⊥平面
⊥平面 (如图).
(如图). 是
是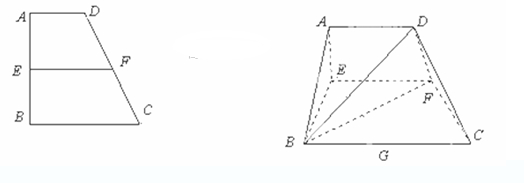
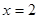 时,求证:
时,求证: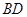 ⊥
⊥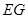 ;
;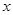 变化时,求三棱锥
变化时,求三棱锥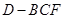 体积的最大值.
体积的最大值. 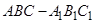 中,
中,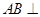 侧面
侧面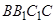 ,已知
,已知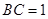 ,
,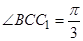 ,
,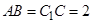 .
.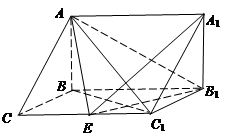
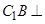 平面
平面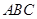 ;
;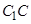 (不包含端点
(不包含端点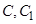 )上确定一点
)上确定一点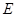 的位置,使得
的位置,使得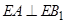 ;
;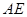 和平面
和平面 的底面
的底面 是正方形,棱
是正方形,棱 底面
底面 =1,
=1,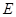 是
是 的中点.
的中点.
 平面
平面 ;
;  的余弦值.
的余弦值.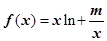 ,曲线
,曲线 在
在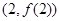 处的切线过点
处的切线过点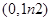 .
.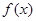 的解析式;
的解析式;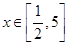 时,求
时,求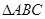 中,
中,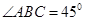 ,
,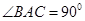 ,
,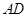 是
是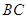 上的高,沿
上的高,沿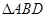 折起,使
折起,使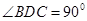 .
.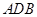 ⊥平面
⊥平面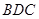 ;
;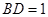 ,求三棱锥
,求三棱锥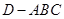 的表面积.
的表面积.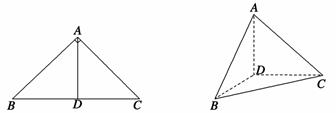
 中,
中, ,
, 的面积为
的面积为 ,则平行四边形
,则平行四边形 .
.
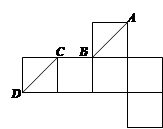
 B.
B. 
 D. AB与CD相交
D. AB与CD相交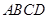 的对棱
的对棱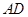 、
、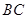 成
成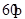 的角,且
的角,且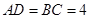 ,平行于
,平行于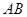 、
、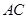 、
、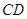 、
、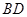 于
于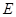 、
、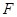 、
、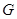 、
、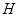 .
.
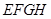 为平行四边形;
为平行四边形;