题目内容
在实数集R上定义运算:

(Ⅰ)求F(x)的解析式;
(Ⅱ)若F(x)在R上是减函数,求实数a的取值范围;
(Ⅲ)若a=-3,在F(x)的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不
存在,说明理由.
解析:(I)由题意,F(x)=f(x)  (a-g(x))…
(a-g(x))…
=ex(a-e-x-2x2)
=aex-1-2x2ex.…
(II)∵F′(x)=aex-2x2ex-4xex=-ex(2x2+4x-a),
当x∈R时,F(x)在减函数,
∴F′(x)≤0对于x∈R恒成立,即
-ex(2x2+4x-a)≤0恒成立, ∵ex>0,
∴2x2+4x-a≥0恒成立,
∴△=16-8(-a) ≤0,
∴a≤-2.
(III)当a=-3时,F(x)= -3ex-1-2x2ex,
设P(x1,y1),Q(x2,y2)是F(x)曲线上的任意两点,
∵F′(x)= -ex(2x2+4x+3)=-ex[2(x+1)2+1]<0,
∴ F′(x1)·F′(x2)>0,
∴F′(x1)·F′(x2)= -1 不成立
∴F(x)的曲线上不存的两点,使得过这两点的切线点互相垂直.

练习册系列答案
相关题目
 且z=2x+y的最小值为4,则实数b的值为( )
且z=2x+y的最小值为4,则实数b的值为( ) ,集合
,集合 ,若
,若 ,则
,则 的取值范围为( )
的取值范围为( ) B.
B.  C.
C.  D.
D. 
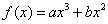 在点
在点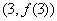 处的切线方程为
处的切线方程为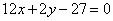 ,且对任意的
,且对任意的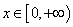 ,
,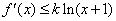 恒成立.
恒成立.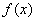 的解析式;(Ⅱ)求实数
的解析式;(Ⅱ)求实数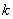 的最小值;
的最小值;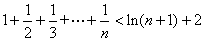 (
(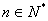 )
)
 ,
,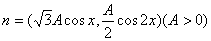 ,函数
,函数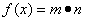 的最大值为6.
的最大值为6. (Ⅱ)将函数y=f(x)的图象像左平移
(Ⅱ)将函数y=f(x)的图象像左平移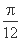 个单位,再将所得图象各点的横坐标缩短为原来的
个单位,再将所得图象各点的横坐标缩短为原来的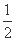 倍,纵坐标不变,得到函数y=g(x)的图象. 求g(x)在
倍,纵坐标不变,得到函数y=g(x)的图象. 求g(x)在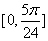 上的值域.
上的值域. 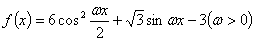 在一个周期内的图像如图所示,A为图像的最高点,B,C为图像与
在一个周期内的图像如图所示,A为图像的最高点,B,C为图像与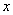 轴的交点,且
轴的交点,且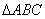 为正三角形.
为正三角形.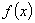 的解析式;
的解析式; 
 的最值
的最值