题目内容
4．已知集合A是函数g（x）=loga[-（x-2a）（x-a）]（a＞0，且a≠1）的定义域，集合B和集合C分别是函数$f（x）=\sqrt{9-{3^x}}$的定义域和值域．（1）求集合A，B，C；
（2）若A∪C=C，求实数a的取值范围．
分析 （1）先求出集合A，根据二次根式的性质求出集合B、C即可；（2）若A∪C=C，则A⊆C，得到关于a的不等式，解出即可．
解答 解：（1）由-（x-2a）（x-a）＞0得（x-2a）（x-a）＜0，又因为a＞0，且a≠1
所以a＜x＜2a，所以A=（a，2a）…（2分）
对于函数$f（x）=\sqrt{9-{3^x}}$，由9-3x≥0得x≤2，B=[2，+∞）…（4分）
所以0＜3x≤9，0≤9-3x＜9，所以$f（x）=\sqrt{9-{3^x}}∈[{0，3}）$，C=[0，3）…（6分）
（2）若A∪C=C，则A⊆C，
则有$\left\{{\begin{array}{l}{a＞0}\\{a≠1}\\{2a≤3}\end{array}}\right.$⇒$0＜a≤\frac{3}{2}$且a≠1，
所以实数a的取值范围是$0＜a≤\frac{3}{2}$且a≠1．…（12分）
点评 本题考查了函数的定义域问题，考查集合的包含关系，考查二次根式以及对数函数的性质，是一道中档题．
练习册系列答案
相关题目
19．为了解某地脐橙种植情况，调研小组在该地某脐橙种植园中随机抽出30棵，每棵挂果情况如下（单位：个）：
157 161 170 180 181 172 162 157 191 182 181 173 174 165 158
164 159 159 168 169 176 178 158 169 176 187 184 175 169 175
（1）完成频数分布表，并作出频率分布直方图．
（2）如果挂果在175个以上（包括175）定义为“高产”，挂果在175个以下（不包括175）定义为“非高产”．用分层抽样的方法从“高产”和“非高产”中抽取5棵，再从这5棵中选2棵，那么至少有一棵是“高产”的概率是多少？
157 161 170 180 181 172 162 157 191 182 181 173 174 165 158
164 159 159 168 169 176 178 158 169 176 187 184 175 169 175
（1）完成频数分布表，并作出频率分布直方图．
| 挂果个数区间 | [155，165） | [165，175） | [175，185） | [185，195] |
| 频数 |
16．
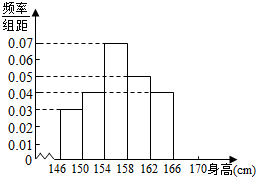为了了解某校高一女生的身高情况，随机抽取M个高一女生测量身高，所得数据整理后列出频率分布如表：
（Ⅰ）求出表中字母m，n所对应的数值；
（Ⅱ）在图中补全频率分布直方图；
（Ⅲ）根据频率分布直方图估计该校高一女生身高的中位数（保留两位小数）
为了了解某校高一女生的身高情况，随机抽取M个高一女生测量身高，所得数据整理后列出频率分布如表：| 组 别 | 频数 | 频率 |
| [146，150） | 6 | 0.12 |
| [150，154） | 8 | 0.16 |
| [154，158） | 14 | 0.28 |
| [158，162） | 10 | 0.20 |
| [162，166） | 8 | 0.16 |
| [166，170） | m | n |
| 合 计 | M | 1 |
（Ⅱ）在图中补全频率分布直方图；
（Ⅲ）根据频率分布直方图估计该校高一女生身高的中位数（保留两位小数）
14．已知集合A={x|y=lg（5-x）}，B={y|y=lg（5-x）}，则A∩B=（ ）
| A． | ∅? | B． | R | C． | （-∞，5） | D． | [0，5] |