题目内容

设F₁，F₂分别是椭圆 $数学公式$ + $数学公式$ =1的左，右焦点，P为椭圆上任一点，点M的坐标为（6，4），则|PM|+|PF₁|的最大值为________．

15
分析：由椭圆的定义可得，|PM|+|PF₁|=2a+|PM|-|PF₂|=2a+|MF₂|，由此可得结论．
解答：由题意F₂（3，0），|MF₂|=5，
由椭圆的定义可得，|PM|+|PF₁|=2a+|PM|-|PF₂|=10+|PM|-|PF₂|≤10+|MF₂|=15，
当且仅当P，F₂，M三点共线时取等号，
故答案为：15．
点评：本题考查椭圆的定义，考查学生分析解决问题的能力，属于基础题．

练习册系列答案

云南省小学毕业总复习与检测系列答案

初中学业水平考试复习指导手册系列答案

点击中考系列答案

预学寓练系列答案

标准大考卷系列答案

单元期中期末试卷系列答案

导学教程高中新课标系列答案

过关检测同步活页试卷系列答案

交大之星课后练系列答案

名师导航好卷100分系列答案

相关题目

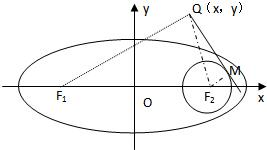设F₁，F₂分别是椭圆C：

=1（m＞0）的左，右焦点．
（1）当P∈C，且

2=0，|PF₁|•|PF₂|=8时，求椭圆C的左，右焦点F₁、F₂．
（2）F₁、F₂是（1）中的椭圆的左，右焦点，已知⊙F₂的半径是1，过动点Q的作⊙F₂切线QM，使得|QF1|=

|QM|（M是切点），如图．求动点Q的轨迹方程．

设F₁、F₂分别是椭圆

+y2=1的左、右焦点．
（I）若M是该椭圆上的一个动点，求

的最大值和最小值；
（II）设过定点（0，2）的直线l与椭圆交于不同两点A、B，且∠AOB为钝角（其中O为坐标原点），求直线l的斜率k的取值范围．

设F₁、F₂分别是椭圆

=1的左、右焦点．
（Ⅰ）若P是该椭圆上的一个动点，求

的最大值和最小值；
（Ⅱ）是否存在过点A（5，0）的直线l与椭圆交于不同的两点C、D，使得|F₂C|=|F₂D|？若存在，求直线l的方程；若不存在，请说明理由．

设F₁，F₂分别是椭圆

+y2=1的左右焦点，过左焦点F₁作直线l与椭圆交于不同的两点A、B．
（Ⅰ）若OA⊥OB，求AB的长；
（Ⅱ）在x轴上是否存在一点M，使得

为常数？若存在，求出M点的坐标；若不存在，说明理由．

设F₁、F₂分别是椭圆E：

=1(a＞b＞0)的左、右焦点，过F₁且斜率为k的直线l与E相交于A、B两点，且|AF₂|、|AB|、|BF₂|成等差数列．
（1）若a=1，求|AB|的值；
（2）若k=1，设点P（0，-1）满足|PA|=|PB|，求椭圆E的方程．