题目内容
求下列函数的定义域
(1)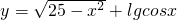 ;
;
(2)
解:(1)欲使其有意义,只须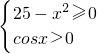 解得
解得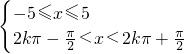
故得x∈[-5,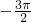 )∪(
)∪( )∪(
)∪( ,5]
,5]
(2)欲使其有意义,只须2|cosx|- sinx-cosx>0 (*)
sinx-cosx>0 (*)
当cosx>0时,(*)可变为cosx- sinx>0即cos(x+
sinx>0即cos(x+ )>0,又0≤x<π,所以
)>0,又0≤x<π,所以 <x+
<x+ <
< 故x∈[0,
故x∈[0, )
)
当cosx<0时,(*)可变为-3cosx- sinx>0,即
sinx>0,即 cosx+sinx<0,可转化为sin(x+
cosx+sinx<0,可转化为sin(x+ )<0
)<0
又0≤x<π,所以π<x+ <
< ,故x∈(
,故x∈( ,π)
,π)
故其定义域为x∈[0, )∪(
)∪( ,π)
,π)
答: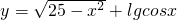 的定义域是[-5,
的定义域是[-5,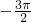 )∪(
)∪( )∪(
)∪( ,5]
,5]
 的定义域是[0,
的定义域是[0, )∪(
)∪( ,π)
,π)
分析:根据使表达式有意义,列出相关的不等式式组即可.
(1)函数有意义,根号下非负,对数式的真数大于0;
(2)先根据真数大于0转化为绝对值不等式,再分类讨论解绝对值不等式,
点评:考查函数定义域的求法,其理论依据是使得函数有意义.
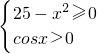 解得
解得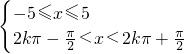
故得x∈[-5,
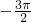 )∪(
)∪( )∪(
)∪( ,5]
,5](2)欲使其有意义,只须2|cosx|-
 sinx-cosx>0 (*)
sinx-cosx>0 (*)当cosx>0时,(*)可变为cosx-
 sinx>0即cos(x+
sinx>0即cos(x+ )>0,又0≤x<π,所以
)>0,又0≤x<π,所以 <x+
<x+ <
< 故x∈[0,
故x∈[0, )
)当cosx<0时,(*)可变为-3cosx-
 sinx>0,即
sinx>0,即 cosx+sinx<0,可转化为sin(x+
cosx+sinx<0,可转化为sin(x+ )<0
)<0又0≤x<π,所以π<x+
 <
< ,故x∈(
,故x∈( ,π)
,π)故其定义域为x∈[0,
 )∪(
)∪( ,π)
,π)答:
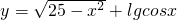 的定义域是[-5,
的定义域是[-5,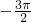 )∪(
)∪( )∪(
)∪( ,5]
,5] 的定义域是[0,
的定义域是[0, )∪(
)∪( ,π)
,π)分析:根据使表达式有意义,列出相关的不等式式组即可.
(1)函数有意义,根号下非负,对数式的真数大于0;
(2)先根据真数大于0转化为绝对值不等式,再分类讨论解绝对值不等式,
点评:考查函数定义域的求法,其理论依据是使得函数有意义.

练习册系列答案
相关题目