题目内容
求过三点A（-2，4），B（-1，3），C（2，6）的圆的方程．
考点：圆的一般方程
专题：直线与圆
分析：设所求圆的方程为x2+y2+Dx+Ey+F=0，将三点坐标代入，即可求得圆的方程．
解答：
解：设圆的方程为x2+y2+Dx+Ey+F=0，则
将A（-2，4），B（-1，3），C（2，6）三点代入可得，
，
∴D=0，E=-10，F=20，
∴所求圆的方程为x2+y2-10y+20=0．
将A（-2，4），B（-1，3），C（2，6）三点代入可得，
|
∴D=0，E=-10，F=20，
∴所求圆的方程为x2+y2-10y+20=0．
点评：本题的考点是圆的方程，主要考查圆的一般方程，解题的关键是利用待定系数法．
练习册系列答案
相关题目
在一个△ABC中，若a=2，b=2，A=30°，那么B等于（ ）
| A、60° |
| B、60°或 120° |
| C、30° |
| D、30°或150° |
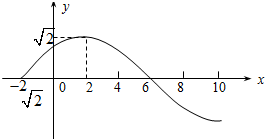已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜