题目内容
已知f(x)=logax(a>1)的导函数是f′(x),记A=f′(a),B=f(a+1)-f(a),C=f′(a+1)则
- A.A>B>C
- B.A>C>B
- C.B>A>C
- D.C>B>A
A
分析:设M坐标为(a,f(a)),N坐标为(a+1,f(a+1)),利用导数及直线斜率的求法得到A、B、C分别为对数函数在M处的斜率,直线MN的斜率及对数函数在N处的斜率,根据对数函数的图象可知大小,得到正确答案.
解答:记M(a,f(a)),N(a+1,f(a+1)),
则由于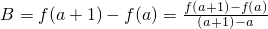 ,表示直线MN的斜率;
,表示直线MN的斜率;
A=f′(a)表示函数f(x)=logax在点M处的切线斜率;
C=f′(a+1)表示函数f(x)=logax在点N处的切线斜率.
所以,A>B>C.
故选A
点评:此题考查学生会利用导数求过曲线上某点切线的斜率,掌握直线斜率的求法,是一道中档题.
分析:设M坐标为(a,f(a)),N坐标为(a+1,f(a+1)),利用导数及直线斜率的求法得到A、B、C分别为对数函数在M处的斜率,直线MN的斜率及对数函数在N处的斜率,根据对数函数的图象可知大小,得到正确答案.
解答:记M(a,f(a)),N(a+1,f(a+1)),
则由于
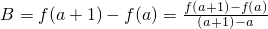 ,表示直线MN的斜率;
,表示直线MN的斜率;A=f′(a)表示函数f(x)=logax在点M处的切线斜率;
C=f′(a+1)表示函数f(x)=logax在点N处的切线斜率.
所以,A>B>C.
故选A
点评:此题考查学生会利用导数求过曲线上某点切线的斜率,掌握直线斜率的求法,是一道中档题.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |