题目内容
(10分)△ABC中,已知三个顶点的坐标分别是A( ,0),B(6,0),C(6,5),
,0),B(6,0),C(6,5),
(1)求AC边上的高线BH所在的直线方程;
(2)求 的角平分线所在直线的方程。
的角平分线所在直线的方程。
解:(1)∵A( ,0),C(6,5)∴
,0),C(6,5)∴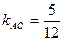
∵BH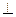 AC ∴
AC ∴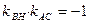 ∴
∴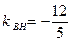
∴高线BH所在的直线方程是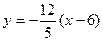
即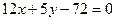 …………………………………………………………..5分
…………………………………………………………..5分
(2)解法1:设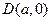 ,又直线AC方程为:
,又直线AC方程为: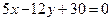 ,
,
点D到直 线AC距离为
线AC距离为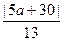 ,点D到直线BC距离为
,点D到直线BC距离为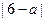 ,
,
则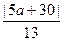 =
=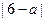 ,解得
,解得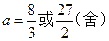
则角平分线CD所在直线方程为: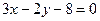 ………………………………………10分
………………………………………10分
解法2:设角平分线CD方程为: ,点B关于直线CD的
,点B关于直线CD的 对称点坐标为
对称点坐标为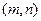 ,则有
,则有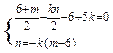 ,解得
,解得
代人直线AC方程: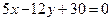 ,得
,得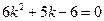 解得
解得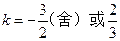
即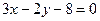

解法3:∵由A,B,C三点坐标可知∠ACB=Rt∠,BC="5,AB=12," ∴AC=13,
延长CB至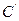 ,使
,使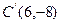 ,
, 此时AC=C
此时AC=C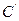 , AC
, AC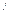 中点P(0, -4),
中点P(0, -4),
则直线CP为 的角平分线所在直线
的角平分线所在直线
∵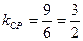 ,
,
∴ 的角平分线所在直线CP的方程为
的角平分线所在直线CP的方程为
即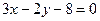
解析

练习册系列答案
相关题目
 :
:
 取何值,直线
取何值,直线 的方程为
的方程为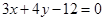 , 求直线
, 求直线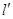 的方程, 使得:
的方程, 使得:  在点x=1处的切线与直线
在点x=1处的切线与直线 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值.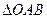 的顶点
的顶点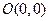 、
、 、
、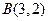 ,
,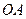 边上的中线所在直线为
边上的中线所在直线为 .
. 关于直线
关于直线 的交点且平行于直线
的交点且平行于直线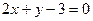 的直线方程. (8分)
的直线方程. (8分)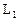 :
: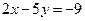 与
与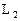 :
: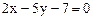 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线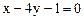 上,已知
上,已知 圆
圆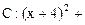
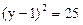 .
.  点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.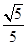 ,求圆的方程.
,求圆的方程.