题目内容
四棱锥P-ABCD的底面是一个正方形,PA与底面垂直,已知PA=3cm,P到BC的距离是5cm,求PC的长.
分析:先根据三垂线定理证明PB⊥BC,然后在直角△PAB中利用勾股定理求出AB长,然后在直角△PBC中利用勾股定理求出PC的长即可.
解答:解:∵ABCD是正方形,
而且PA⊥平面ABCD,
∴PB⊥BC(三垂线定理)
在直角△PAB中AB=
=
=4(cm),
在直角△PBC中PC=
=
=
(cm).
而且PA⊥平面ABCD,
∴PB⊥BC(三垂线定理)
在直角△PAB中AB=
| PB2-PA2 |
| 52-32 |
在直角△PBC中PC=
| PB2+BC2 |
| 52+42 |
| 41 |
点评:本题主要考查了直线与平面垂直的性质,以及三垂线定理的应用,同时考查了计算能力,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
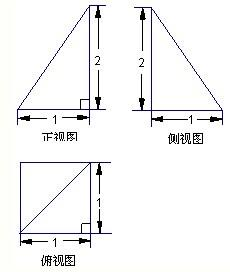 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
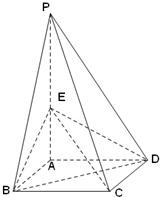 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: