题目内容
命题P“方程
有解”是命题Q“方程x2-2x+a=0无实根”的______条件．
- A.充分不必要
- B.必要不充分
- C.充要
- D.既不充分也不必要
B
分析：由指数和对数的关系可化简方程，分离a，由基本不等式可得a≥1，再由△＜0可得a＞1，由集合的包含关系可得答案．
解答：方程可化为
=a-2x，
整理可得a=
≥2
=1，
当且仅当
，即x=-1时取等号，
故可得a≥1；
而方程x2-2x+a=0无实根可得△=（-2）2-4a＜0，
解得a＞1，
又因为集合{a|a≥1}真包含{a|a＞1}，
所以P是Q的必要不充分条件
故选B
点评：本题考查充要条件的判断，涉及基本不等式和一元二次方程根的情况，属基础题．
分析：由指数和对数的关系可化简方程，分离a，由基本不等式可得a≥1，再由△＜0可得a＞1，由集合的包含关系可得答案．
解答：方程
可化为=a-2x，整理可得a=
≥2=1，当且仅当
，即x=-1时取等号，故可得a≥1；
而方程x2-2x+a=0无实根可得△=（-2）2-4a＜0，
解得a＞1，
又因为集合{a|a≥1}真包含{a|a＞1}，
所以P是Q的必要不充分条件
故选B
点评：本题考查充要条件的判断，涉及基本不等式和一元二次方程根的情况，属基础题．
练习册系列答案
相关题目
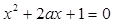有两个大于-1的实数根，已知命题q：关于x的不等式
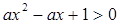的解集是R,若“p或q”与“
”
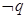同时为真命题，求实数a的取值范围(12分)
有解”是命题Q“方程x2-2x+a=0无实根”的（ ）条件．