题目内容
18.已知等比数列{bn}满足b3=2,b2+b4=$\frac{20}{3}$,求数列{bn}的通项公式.分析 设出等比数列的首项为b1和公比为q,由已知列方程组求得首项和公比,代入等比数列的通项公式得答案.
解答 解:设等比数列的首项为b1,公比为q,
由b3=2,b2+b4=$\frac{20}{3}$,
得$\left\{\begin{array}{l}{{b}_{1}{q}^{2}=2}\\{{b}_{1}(q+{q}^{3})=\frac{20}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{b}_{1}=18}\\{q=\frac{1}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{{b}_{1}=\frac{2}{9}}\\{q=3}\end{array}\right.$.
∴${b}_{n}=18×(\frac{1}{3})^{n-1}$或${b}_{n}=\frac{2}{9}×{3}^{n-1}=2×{3}^{n-3}$.
点评 本题考查等比数列的通项公式,考查方程组的解法,是基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
8.设全集U=R,集合A={x|0<x<2},B={x|x<1},则集合(∁UA)∩B=( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (2,+∞) | D. | [2,+∞) |
6.从5人中选3人参加座谈会,其中甲必须参加,则不同的选法有( )
| A. | 12种 | B. | 6种 | C. | 5种 | D. | 4种 |
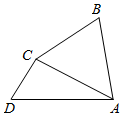 如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).
如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).