Question

【题目】设是数列1，，，…，的各项和，，.

（1）设，证明：在内有且只有一个零点；

（2）当时，设存在一个与上述数列的首项、项数、末项都相同的等差数列，其各项和为，比较与的大小，并说明理由；

（3）给出由公式推导出公式的一种方法如下：在公式中两边求导得：，所以成立，请类比该方法，利用上述数列的末项的二项展开式证明：时（其中表示组合数）

Answer 1

【答案】（1）证明见解析；（2），理由见解析；（3）证明见解析.

【解析】

（1）依题意可得，求出导函数说明其单调性，再由等比数列前项和得，又；

（2）由题意，，设，然后利用导数研究其单调性即可得证；

（3）

由二项展开式得，

两边求导：，

再令，代入可证；

解：（1），

，

由于，故，

因此，在单调递增，

又，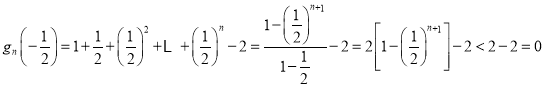

，

所以在内有且只有一个零点.

（2）由题意，.

设.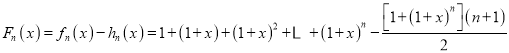

当时，，，

当时，，

此时

，

所以单调递增，，，

当时，，

，

所以单调递减，，.

综上，时，；

且时，.

（3）数列的末项为，

由二项展开式得，

两边求导：，

取，得，

两边乘以，得，

即.