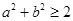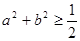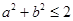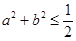题目内容
若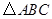 内有一点
内有一点 ,满足
,满足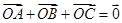 ,且
,且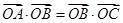 ,则
,则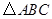 一定是( )
一定是( )
| A.钝角三角形 | B.直角三角形 | C.等边三角形 | D.等腰三角形 |
D
解析试题分析:因为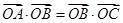 ,所以
,所以 ,所以
,所以 ,所以O在AC的高线上,又
,所以O在AC的高线上,又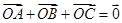 ,所以
,所以 ,设AC的中点为D,所以
,设AC的中点为D,所以 ,故O在AC的中线上,所以三角形一定是等腰三角形.选D.
,故O在AC的中线上,所以三角形一定是等腰三角形.选D.
考点:平面向量数量积的运算
点评:本题考查向量的运算在三角形中的应用,考查学生利用所学知识分析问题,解决问题的能力.

练习册系列答案
相关题目
对于任意向量 、
、 、
、 ,下列命题中正确的是( )
,下列命题中正确的是( )
A. | B. | C. | D. |
已知若

 和
和 夹角为钝角,则
夹角为钝角,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
若 是非零向量且满足
是非零向量且满足 ,
, ,则
,则 与
与 的夹角是
的夹角是
A. | B. | C. | D. |
已知向量 ,
, ,若
,若 ,则实数
,则实数 的值为( ).
的值为( ).
A. | B. | C. | D. |
已知平面向量 满足
满足 ,且
,且 ,则向量
,则向量 与
与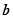 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
在四边形ABCD中,若 ,且
,且 ,则( )
,则( )
| A.ABCD是矩形 | B.ABCD是正方形 |
| C.ABCD是菱形 | D.ABCD是平行四边形 |
已知 为平面上不共线的三点,
为平面上不共线的三点, 是△ABC的垂心,动点
是△ABC的垂心,动点 满足
满足 ,则点
,则点 一定为△ABC的( )
一定为△ABC的( )
A. 边中线的中点 边中线的中点 | B. 边中线的三等分点(非重心) 边中线的三等分点(非重心) |
| C.重心 | D. 边的中点 边的中点 |
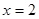 与双曲线
与双曲线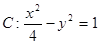 的渐近线交于
的渐近线交于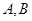 两点,设
两点,设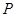 为双曲线
为双曲线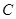 上的任意一点,若
上的任意一点,若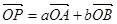 (
(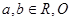 为坐标原点),则下列不等式恒成立的是( )
为坐标原点),则下列不等式恒成立的是( )