题目内容
已知等差数列 满足a1=1,a3=6,若对任意的n∈N*,数列{bn}满足bn,2an+1,bn+1依次成等比数列,且b1=4.
满足a1=1,a3=6,若对任意的n∈N*,数列{bn}满足bn,2an+1,bn+1依次成等比数列,且b1=4.
(1)求an,bn
(2)设Sn=(-1)b1+(-1)2b2+…+(-1)nbn,n∈N*,证明:对任意的n∈N*, .
.
解:(1)设数列 的公差d,依题意该数列的第一项为
的公差d,依题意该数列的第一项为 =1,第三项为
=1,第三项为 ,
,
∴2=1+(3-1)d,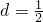 .
.
∴ ,
,
∴ ,
,
∵bn,2an+1,bn+1依次成等比数列,且b1=4.
∴bn•bn+1=4an+12,
∴bn•bn+1=(n+2)2(n+1)2,
∴ =1,n∈N*.
=1,n∈N*.
令 ,
,
则cncn+1=1,∴ ,且cn≠0.
,且cn≠0.
∵ =
= ,
,
∴ ,
,
∴ ,
,
∴bn=(n+1)2.
(2)当n是偶数时,
Sn=(-1)•b1+(-1)2•b2+…+(-1)nbn
=-22+32-42+52-62+72-…-n2+(n+1)2
=5+9+13+…+(2n+1)
= .
.
∴ =
= =
= ,
,
∴ .
.
当n是奇数时,
Sn=(-1)•b1+(-1)2•b2+…+(-1)nbn
=-22+32-42+52-62+72-82+…+n2-(n+1)2
=5+9+13+…+(2n-1)-(n+1)2
=
∴ =
= ═
═ ,
,
∴ .
.
综上所述,对任意的n∈N*, .
.
分析:(1)设数列 的公差d,依题意该数列的第一项为
的公差d,依题意该数列的第一项为 =1,第三项为
=1,第三项为 ,所以
,所以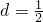 .由此能求出
.由此能求出 .由bn,2an+1,bn+1依次成等比数列,且b1=4.知bn•bn+1=4an+12,
.由bn,2an+1,bn+1依次成等比数列,且b1=4.知bn•bn+1=4an+12, ,n∈N*.由此能求出bn=(n+1)2.
,n∈N*.由此能求出bn=(n+1)2.
(2)当n是偶数时,Sn=(-1)•b1+(-1)2•b2+…+(-1)nbn=-22+32-42+52-62+72-…-n2+(n+1)2= .所以
.所以 .当n是奇数时,
.当n是奇数时, =
= ,所以
,所以 ,综上所述,对任意的n∈N*,
,综上所述,对任意的n∈N*, .
.
点评:本题考查数列的通项公式的求法和证明对任意的n∈N*, .解题时要认真审题,注意构造法和分类讨论思想的合理运用.计算量大,容易出错,要注意计算能力的培养.
.解题时要认真审题,注意构造法和分类讨论思想的合理运用.计算量大,容易出错,要注意计算能力的培养.
 的公差d,依题意该数列的第一项为
的公差d,依题意该数列的第一项为 =1,第三项为
=1,第三项为 ,
,∴2=1+(3-1)d,
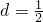 .
.∴
 ,
,∴
 ,
,∵bn,2an+1,bn+1依次成等比数列,且b1=4.
∴bn•bn+1=4an+12,
∴bn•bn+1=(n+2)2(n+1)2,
∴
 =1,n∈N*.
=1,n∈N*.令
 ,
,则cncn+1=1,∴
 ,且cn≠0.
,且cn≠0.∵
 =
= ,
,∴
 ,
,∴
 ,
,∴bn=(n+1)2.
(2)当n是偶数时,
Sn=(-1)•b1+(-1)2•b2+…+(-1)nbn
=-22+32-42+52-62+72-…-n2+(n+1)2
=5+9+13+…+(2n+1)
=
 .
.∴
 =
= =
= ,
,∴
 .
.当n是奇数时,
Sn=(-1)•b1+(-1)2•b2+…+(-1)nbn
=-22+32-42+52-62+72-82+…+n2-(n+1)2
=5+9+13+…+(2n-1)-(n+1)2
=

∴
 =
= ═
═ ,
,∴
 .
.综上所述,对任意的n∈N*,
 .
.分析:(1)设数列
 的公差d,依题意该数列的第一项为
的公差d,依题意该数列的第一项为 =1,第三项为
=1,第三项为 ,所以
,所以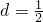 .由此能求出
.由此能求出 .由bn,2an+1,bn+1依次成等比数列,且b1=4.知bn•bn+1=4an+12,
.由bn,2an+1,bn+1依次成等比数列,且b1=4.知bn•bn+1=4an+12, ,n∈N*.由此能求出bn=(n+1)2.
,n∈N*.由此能求出bn=(n+1)2.(2)当n是偶数时,Sn=(-1)•b1+(-1)2•b2+…+(-1)nbn=-22+32-42+52-62+72-…-n2+(n+1)2=
 .所以
.所以 .当n是奇数时,
.当n是奇数时, =
= ,所以
,所以 ,综上所述,对任意的n∈N*,
,综上所述,对任意的n∈N*, .
.点评:本题考查数列的通项公式的求法和证明对任意的n∈N*,
 .解题时要认真审题,注意构造法和分类讨论思想的合理运用.计算量大,容易出错,要注意计算能力的培养.
.解题时要认真审题,注意构造法和分类讨论思想的合理运用.计算量大,容易出错,要注意计算能力的培养. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足a1=1,a3=6,若对任意的n∈N*,数列{bn}满足bn,2an+1,bn+1依次成等比数列,且b1=4.
满足a1=1,a3=6,若对任意的n∈N*,数列{bn}满足bn,2an+1,bn+1依次成等比数列,且b1=4. .
. 满足a1=1,a3=6,若对任意的n∈N*,数列{bn}满足bn,2an+1,bn+1依次成等比数列,且b1=4.
满足a1=1,a3=6,若对任意的n∈N*,数列{bn}满足bn,2an+1,bn+1依次成等比数列,且b1=4. .
.