题目内容
一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.(1)判断f1(x)=![]() ,f2(x)=x,f3(x)=x2中,哪些是“保三角形函数”,哪些不是,并说明理由;
,f2(x)=x,f3(x)=x2中,哪些是“保三角形函数”,哪些不是,并说明理由;
(2)如果g(x)是定义在R上的周期函数,且值域为(0,+∞),证明g(x)不是“保三角形函数”;
(3)若函数F(x)=sinx,x∈(0,A)是“保三角形函数”,求A的最大值.
(可以利用公式sinx+siny=2sin![]() cos
cos![]() )
)
(1)解:f1(x),f2(x)是“保三角形函数”,f3(x)不是“保三角形函数”.
任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,
由于![]() +
+![]() >
>![]() >
>![]() >0,所以f1(x),f2(x)是“保三角形函数”.
>0,所以f1(x),f2(x)是“保三角形函数”.
对于f3(x),3,3,5可作为一个三角形的三边长,但32+32<52,所以不存在三角形以32,32,52为三边长,故f3(x)不是“保三角形函数”.
(2)证明:设T>0为g(x)的一个周期,由于其值域为(0,+∞),所以,存在n>m>0,使得g(m)=1,g(n)=2.
取正整数λ>![]() ,可知λT+m,λT+m,n这三个数可作为一个三角形的三边长,但g(λT+m)=1,g(λT+m)=1,g(n)=2不能作为任何一个三角形的三边长.
,可知λT+m,λT+m,n这三个数可作为一个三角形的三边长,但g(λT+m)=1,g(λT+m)=1,g(n)=2不能作为任何一个三角形的三边长.
故g(x)不是“保三角形函数”.
(3)解:A的最大值为![]() .
.
一方面,若A>![]() ,下证F(x)不是“保三角形函数”.
,下证F(x)不是“保三角形函数”.
取![]() ,
,![]() ,
,![]() ∈(0,A),显然这三个数可作为一个三角形的三边长,但sin
∈(0,A),显然这三个数可作为一个三角形的三边长,但sin![]() =1,sin
=1,sin![]() =
=![]() ,sin
,sin![]() =
=![]() 不能作为任何一个三角形的三边长,故F(x)不是“保三角形函数”.
不能作为任何一个三角形的三边长,故F(x)不是“保三角形函数”.
另一方面,以下证明A=![]() 时,F(x)是“保三角形函数”.
时,F(x)是“保三角形函数”.
对任意三角形的三边a,b,c,若a,b,c∈(0,![]() ),则分类讨论如下:
),则分类讨论如下:
①a+b+c≥2π,
此时a≥2π-b-c>2π![]() =
=![]() ,同理,b,c>
,同理,b,c>![]() ,
,
∴a,b,c∈(![]() ,
,![]() ),故sina,sinb,sinc∈(
),故sina,sinb,sinc∈(![]() ,1],
,1],
sina+sinb>![]() +
+![]() =1≥sinc.
=1≥sinc.
同理可证其余两式.
∴sina,sinb,sinc可作为某个三角形的三边长.
②a+b+c<2π.
此时,![]() <π,可得如下两种情况:
<π,可得如下两种情况:
![]() ≤
≤![]() 时,由于a+b>c,∴0<
时,由于a+b>c,∴0<![]() <
<![]() ≤
≤![]() .
.
由sinx在(0,![]() ]上的单调性可得0<sin
]上的单调性可得0<sin![]() <sin
<sin![]() ≤1;
≤1;
![]() >
>![]() 时,0<
时,0<![]() <π
<π![]() <
<![]() ,同样,由sinx在[0,
,同样,由sinx在[0,![]() ]上的单调性可得0<sin
]上的单调性可得0<sin![]() <sin
<sin![]() <1.
<1.
总之,0<sin![]() <sin
<sin![]() ≤1.
≤1.
又由|a-b|<c<![]() 及余弦函数在(0,π)上单调递减,得cos
及余弦函数在(0,π)上单调递减,得cos![]() =cos
=cos![]() >cos
>cos![]() >cos
>cos![]() >0,
>0,
∴sina+sinb=2sin![]() cos
cos![]() >2sin
>2sin![]() cos
cos![]() =sinc.
=sinc.
同理可证其余两式,所以sina,sinb,sinc也是某个三角形的三边长.故A=![]() 时,F(x)是“保三角形函数”.
时,F(x)是“保三角形函数”.
综上,A的最大值为![]() .
.
说明:其他正确解法按相应步骤给分.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| 1 |
| x2+1 |
| 1 |
| x |
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||||
f(x)-
|
… | |||||||
g(x)-
|
… |
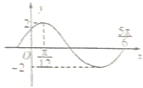 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 4 |
| A、1 | ||
B、
| ||
| C、-1 | ||
D、-
|
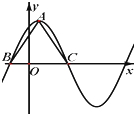 函数
函数 函数
函数