题目内容
4.求函数f(x)=sin2x+$\sqrt{3}$cos2x在区间[0,π]上的零点之和.分析 令f(x)=0,利用正切函数的性质求出函数的零点,即可得到结论.
解答 解:由f(x)=sin2x+$\sqrt{3}$cos2x=0,得sin2x=-$\sqrt{3}$cos2x,
即tan2x=-$\sqrt{3}$,
解得2x=kπ-$\frac{π}{3}$,
即x=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z;
∵0≤x≤π,
∴当k=1时,x=$\frac{π}{3}$,
当k=2时,x=$\frac{5π}{6}$,
∴函数f(x)在区间[0,π]上的零点之和为$\frac{π}{3}$+$\frac{5π}{6}$=$\frac{7π}{6}$.
点评 本题主要考查了函数零点的应用问题,根据正切函数的性质求出x的值是解决本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
12.据市场调查结果,预测某种家用商品从2014年初开始,n个月内累计的需求量Sn(万件)近似地满足Sn=2ln2-n3(n=1,2,…,12),按此预测在本年度内,需求量最大的月份是( )
| A. | 5月、6月 | B. | 6月、7月 | C. | 7月、8月 | D. | 8月、9月 |
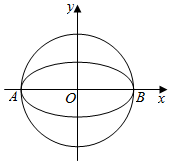 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.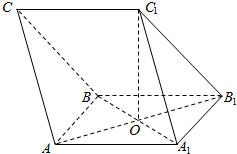 如图,在三棱柱ABC-A1B1C1中,O是正方形AA1B1B的中心,AB=2$\sqrt{2}$,C1O⊥平面AA1B1B,且C1O=2.
如图,在三棱柱ABC-A1B1C1中,O是正方形AA1B1B的中心,AB=2$\sqrt{2}$,C1O⊥平面AA1B1B,且C1O=2.