题目内容
设{an}是公差d≠0的等差数列，且
恰好构成等比数列，其中k1=1,k2=5,k3=17，求k1+k2+…+kn.
思路分析：欲求k1+k2+…+kn需找出数列{kn}的规律，即通项公式.可以看出具有双重性，它是{an}的第kn项又是等比数列
的第 n项.
解：由题知a1，a5,a17成等比数列，
∴(a1+4d)2=a1(a1+16d) (d≠0).
则a1=2d.
∴
的公比q=
∴在等差数列中，
=a1+(kn-1)·d=(kn+1)d.
在等比数列中，
=a1·qn-1=a1·3n-1=2d·3n-1.
从而(kn+1)d=2d·3n-1得kn=2·3n-1-1.
∴k1+k2+…+kn=(2·30-1)+(2·31-1)+…+(2·3n-1-1)
=2(1+3+32+…+3n-1)-n
=2·
-n
=3n-n-1.
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
，求数列{an}的通项公式；
的等差中项？证明你的结论.
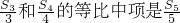，求数列{an}的通项公式；