题目内容
设{an}是公差d≠0的等差数列，Sn是其前n项的和．（1）若a1=4，且
| S3 |
| 3 |
| S4 |
| 4 |
| S5 |
| 5 |
（2）是否存在p，q∈N*，且p≠q，使得Sp+q是S2p和S2q的等差中项？证明你的结论．
分析：（1）先由
和
的等比中项是
求得d，再求解通项公式；
（2）由Sp+q是S2p和S2q的等差中项整理化简，为（p-q）d=0，再由条件分析．
| S3 |
| 3 |
| S4 |
| 4 |
| S5 |
| 5 |
（2）由Sp+q是S2p和S2q的等差中项整理化简，为（p-q）d=0，再由条件分析．
解答：解：（1）∵
和
的等比中项是
∴(
)2 =
•
又∵a1=4
∴d=2.4
（2）不存在
∵Sp+q是S2p和S2q的等差中项
∴2Sp+q=S2p+S2q
∴整理得（p-q）d=0
∵p≠q，d≠0
∴不存在
| S3 |
| 3 |
| S4 |
| 4 |
| S5 |
| 5 |
∴(
| s5 |
| 5 |
| s3 |
| 3 |
| s4 |
| 4 |
又∵a1=4
∴d=2.4
（2）不存在
∵Sp+q是S2p和S2q的等差中项
∴2Sp+q=S2p+S2q
∴整理得（p-q）d=0
∵p≠q，d≠0
∴不存在
点评：本题主要考查等比数列的等比中项以及等差数列与等比数列综合运用的能力．
练习册系列答案
名校课堂系列答案
相关题目
，求数列{an}的通项公式；
的等差中项？证明你的结论.
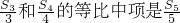，求数列{an}的通项公式；