题目内容
10.过棱长为1的正方体的一个顶点作该正方体的截面,若截面形状为四边形,则下列选项中不可能为该截面面积的是( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 设过顶点A作正方体的截面AEFG与底面ABCD所成的角为θ,利用关系式:$\frac{{S}_{底面ABCD}}{{S}_{截面AEFG}}$=cosθ,得出S截面AEFG>1又当截面AEFG是正方体的对角面AB1C1D时,其面积最大,最大为$\sqrt{2}$,从而得到截面面积的取值范围.
解答 解;如图所示,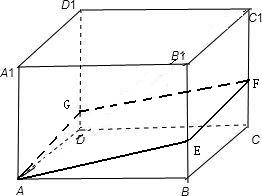 ,
,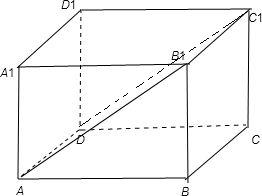 ,
,
设过顶点A作正方体的截面AEFG与底面ABCD所成的角为θ,
则有:$\frac{{S}_{底面ABCD}}{{S}_{截面AEFG}}$=cosθ,
∴S截面AEFG=$\frac{{S}_{底面ABCD}}{cosθ}$>1,
又当截面AEFG是正方体的对角面AB1C1D时,其面积最大,最大为$\sqrt{2}$,
则截面面积的取值范围是 (1,$\sqrt{2}$].
故选:D
点评 本小题主要考查棱柱的结构特征、正方体的结构特征的应用、正方体的截面等基础知识,考查空间想象能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
15.正方体的截面不可能是:①钝角三角形;②直角三角形;③菱形;④正五边形;⑤正六边形.下述选项正确的是( )
| A. | ①②⑤ | B. | ①②④ | C. | ②③④ | D. | ③④⑤ |
2.已知3a=5b=A,且$\frac{1}{a}$+$\frac{1}{b}$=2,则A的值是( )
| A. | 15 | B. | $\sqrt{15}$ | C. | ±$\sqrt{15}$ | D. | 22 |
20.在空间直角坐标系Oxyz中,点A(a,a,a),B(a,a,0),C(0,0,a).其中a>0,则△ABC为( )
| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 正三角形 | D. | 钝角三角形 |
 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=4,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=4,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.