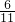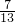题目内容
x+y+z=1,F=2x2+y2+3z2的最小值为( )
分析:利用柯西不等式得,(2x2+y2+3z2)(
+1+
)≥(2x2×
+y2×1+3z2×
)22,利用条件可求.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:由柯西不等式得,(2x2+y2+3z2)(
+1+
)≥(2x2×
+y2×1+3z2×
)22=(x+y+z)2=1
∴2x2+y2+3z2≥
,即F的最小值为
故选A.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴2x2+y2+3z2≥
| 6 |
| 11 |
| 6 |
| 11 |
故选A.
点评:柯西不等式的特点:一边是平方和的积,而另一边为积的和的平方,因此,当欲证不等式的一边视为“积和结构”或“平方和结构”,再结合不等式另一边的结构特点去尝试构造.

练习册系列答案
相关题目
(2009•普宁市模拟)为了确保神州七号飞船发射时的信息安全,信息须加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
|